Nội Dung
Hướng dẫn giải Bài §8. Phép đồng dạng, Chương I. Phép dời hình và phép đồng dạng trong mặt phẳng, sách giáo khoa Hình học 11. Nội dung bài giải bài 1 2 3 4 trang 33 sgk Hình học 11 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập hình học có trong SGK để giúp các em học sinh học tốt môn toán lớp 11.
Lý thuyết
1. Định nghĩa phép đồng dạng
Phép biến hình \(f\) được gọi là phép đồng dạng tỉ số \(k\), \((k>0)\), nếu với hai điểm \(M, N\) bất kì và ảnh \(M’, N’\) tương ứng của chúng, ta luôn có \(M’N’ = kMN\)
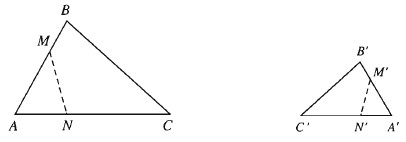
\(\left\{ \begin{array}{l}F(M) = M’\\F(N) = N’\end{array} \right. \Rightarrow M’N’ = k.MN\,\,(k > 0)\)
Nhận xét:
Phép dời hình là phép đồng dạng tỉ số \(1\).
Phép vị tự tỉ số \(k\) là phép đồng dạng tỉ số \(|k|\).
Nếu thực hiện liên tiếp phép đồng dạng tỉ số \(k\) và phép đồng dạng tỉ số \(p\) ta được phép đồng dạng tỉ số \(pk\).
2. Tính chất của phép đồng dạng
a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữ các điểm ấy.
b) Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng có độ dài bằng \(a\) thành đoạn thẳng có độ dài bằng \(ka\).
c) Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là \(k\), biến góc thành góc bằng nó.
d) Biến đường tròn bán kình \(R\) thành đường tròn bán kính \(k R\).
3. Hình đồng dạng
Hai hình được gọi là đồng dạng với nhau nếu có một phép đồng dạng biến hình này thành hình kia.
So sánh phép dời hình, vị tự V(O,k), đồng dạng tỉ số k:
Giống nhau:
Biến ba điểm thẳng hàng thành ba điểm thẳng hàng (và không làm thay đổi thứ tự của ba điểm đó).
Biến đường thẳng thành đường thẳng, tia thành tia, biến góc thành góc bằng nó.
Sự khác nhau:
| Phép dời hình | Phép vị tự | Phép đồng dạng |
| Biến đoạn thẳng thành đoạn thẳng bằng nó.
Biến tam giác thành tam giác bằng tam giác đó. Biến đường tròn thành đường tròn có bán kính bằng đường tròn đã cho. |
Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với |k|.
Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là |k|. Biến đường tròn thành đường tròn có bán kính có bán kính là |k|R. |
Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với k.
Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là k. Biến đường tròn thành đường tròn có bán kính có bán kính là kR. |
Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong mục hoạt động của học sinh trên lớp sgk Hình học 11.
Câu hỏi
1. Trả lời câu hỏi 1 trang 30 sgk Hình học 11
Chứng minh nhận xét 2.
Phép vị tự tỉ số $k$ là phép đồng dạng tỉ số $|k|.$
Trả lời:
Phép vị tự tâm $O$, tỉ số $k$ biến điểm $M, N$ thành $2$ điểm $M’,N’$ sao cho:
\(\left\{ \matrix{
\overrightarrow {OM’} = k\overrightarrow {OM} \hfill \cr
\overrightarrow {ON’} = k\overrightarrow {ON} \hfill \cr} \right.\)
\(\eqalign{
& \Rightarrow \overrightarrow {M’N’} = \overrightarrow {ON’} – \overrightarrow {OM’} = k\overrightarrow {ON’} – k\overrightarrow {OM’} = k\overrightarrow {MN} \cr
& \Rightarrow |\overrightarrow {M’N’} |\, = \,|k\overrightarrow {MN} |\, \Rightarrow M’N’ = |k|MN \cr} \)
Vậy phép vị tự tỉ số $k$ là phép đồng dạng tỉ số $|k|.$
2. Trả lời câu hỏi 2 trang 30 sgk Hình học 11
Chứng minh nhận xét 3.
Nếu thực hiện liên tiếp phép đồng dạng tỉ số $k$ và phép đồng dạng tỉ số $p$ ta được phép đồng dạng tỉ số $pk$.
Trả lời:
– Phép đồng dạng tỉ số $k$ biến $2$ điểm $M, N$ thành $2$ điểm $M’,N’$ sao cho $M’N’ = kMN$
– Phép đồng dạng tỉ số $b$ biến $2$ điểm $M’,N’$ thành $2$ điểm $M”,N”$ sao cho $M”N” = pM’N’$
$⇒ M”N” = pkMN$
Vậy: Nếu thực hiện liên tiếp phép đồng dạng tỉ số $k$ và phép đồng dạng tỉ số $p$ ta được phép đồng dạng tỉ số $pk$
3. Trả lời câu hỏi 3 trang 31 sgk Hình học 11
Chứng minh tính chất a.
Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.
Trả lời:
Phép đồng dạng tỉ số $k$ biến $3$ điểm $A, B, C$ thẳng hàng thành $3$ điểm $A’,B’,C’$ sao cho:
$A’B’ = kAB, B’C’ = kBC, A’C’ = kAC$
$A, B, C$ thẳng hàng và $B$ nằm giữa $A, C ⇔ AB + BC = AC$
Do đó $kAB + kBC = kAC$ hay $A’B’ + B’C’ = A’C’$
$⇒ A’, B’, C’$ thẳng hàng và $B’$ nằm giữa $A’, C’$
4. Trả lời câu hỏi 4 trang 31 sgk Hình học 11
Gọi $A’, B’$ lần lượt là ảnh của $A, B$ qua phép đồng dạng $F$, tỉ số $k$. Chứng minh rằng nếu $M$ là trung điểm của $AB$ thì $M’ = F(M)$ là trung điểm của $A’B’.$
Trả lời:
$A’, B’$ lần lượt là ảnh của $A, B$ qua phép đồng dạng $F$, tỉ số $k ⇒ A’B’= kAB$
$M’ = F(M) ⇒ A’M’ = kAM$
$M$ là trung điểm $AB ⇒ AM = \frac{1}{2} AB ⇒ kAM = \frac{1}{2} kAB$ hay $A’M’= \frac{1}{2} A’B’$
Vậy $M’$ là trung điểm của $A’B’$
5. Trả lời câu hỏi 5 trang 33 sgk Hình học 11
Hai đường tròn (hai hình vuông, hai hình chữ nhật) bất kì có đồng dạng với nhau không?
Trả lời:
Hai đường tròn (hai hình vuông, hai hình chữ nhật) bất kì có đồng dạng với nhau.
Dưới đây là phần Hướng dẫn giải bài 1 2 3 4 trang 33 sgk Hình học 11. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập hình học 11 kèm bài giải chi tiết bài 1 2 3 4 trang 33 sgk Hình học 11 của Bài §8. Phép đồng dạng trong Chương I. Phép dời hình và phép đồng dạng trong mặt phẳng cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 1 trang 33 sgk Hình học 11
Cho tam giác $ABC$. Xác định ảnh của nó qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm $B$ tỉ số \(\frac{1}{2}\) và phép đối xứng qua đường trung trực của $BC$
Bài giải:
♦ Cách 1:

Gọi tam giác $A’B’C’$ là ảnh của tam giác $ABC$ qua \(V_ {\left ( B, \frac{1}{2} \right )}\), khi đó \(V_ {\left ( B, \frac{1}{2} \right )} \ (B)=B\) hay $B’$ trùng với $B$.
\(A’=V_ {\left ( B, \frac{1}{2} \right )} \ (A)\Leftrightarrow \overrightarrow{BA’}=\frac{1}{2}\overrightarrow{BA}\) hay $A’$ là trung điểm của $BA.$
\(C’=V_ {\left ( B, \frac{1}{2} \right )} \ (C)\Leftrightarrow \overrightarrow{BC’}=\frac{1}{2}\overrightarrow{BC}\) hay $C$’ là trung điểm của $BC$.
Gọi tam giác $A”B”C”$ là ảnh của tam giác $A’B’C’$ qua phép đối xứng qua đường trung trực $d$ của $BC$, khi đó
$Đd (B’) = C$ hay $B”$ trùng với $C.$
$Đd(C’) = C’$ hay $C”$ trùng với $C’.$
Gọi $H$ là hình chiếu vuông góc của $A’$ trên $d. A’$ là điểm thoả mãn điều kiện \(\Leftrightarrow \overrightarrow{HA”}=-\overrightarrow{HA’}\) hay $H$ là trung điểm của $A’A”.$
Vậy tam giác $A”B”C”$ vừa dựng trên là ảnh của tam giác $ABC.$
♦ Cách 2:

\({V_{\left( {B;\frac{1}{2}} \right)}}\left( A \right) = A’ \Rightarrow \overrightarrow {BA’} = \frac{1}{2}\overrightarrow {BA} \Rightarrow A’\) là trung điểm của AB.
Tương tự ta có C’ là trung điểm của BC và \({V_{\left( {B;\frac{1}{2}} \right)}}\left( C \right) = C’\)
\({V_{\left( {B;\frac{1}{2}} \right)}}\left( {\Delta ABC} \right) = \Delta A’BC’\).
Phép đối xứng qua đường trung trực của \(BC\) biến tam giác \(A’BC’\) thành tam giác \(A”CC’\).
Vậy ảnh của tam giác ABC qua phép đồng dạng đã cho là tam giác \(A”CC’\).
2. Giải bài 2 trang 33 sgk Hình học 11
Cho hình chữ nhật $ABCD, AC$ và $BD$ cắt nhau tại $I$. Gọi $H, K, L$ và $J$ lần lượt là trung điểm của $AD, BC, KC$ và $IC$. Chứng minh hai hình thang $JLKI$ và $IHDC$ đồng dạng với nhau.
Bài giải:

Xét \(\Delta CKI\) ta có LJ là đường trung bình nên \(LJ=\frac{1}{2}KI=\frac{1}{2}IH\)
Do đó \(LJ=\frac{1}{2}IH (1)\)
Xét \(\Delta BCD\) ta có KI là đường trung bình nên \(KI=\frac{1}{2}DC \ (2)\)
và \(KL=\frac{1}{2}KC=\frac{1}{2}HD \ (3)\)
\(IJ=\frac{1}{2} IC \ \ (4)\)
Từ (1), (2), (3), (4) ta có: Hình thang $JLKI$ là ảnh của hình thang $IHDC$ qua phép đồng dạng tỉ số \(\frac{1}{2}\).
Vậy hai hình thang $JLKI$ và hình thang $IHDC$ là đồng dạng với nhau.
3. Giải bài 3 trang 33 sgk Hình học 11
Trong mặt phẳng $Oxy$ cho điểm \(I (1;1)\) và đường trong tâm $I$ bán kính $2$. Viết phương trình của đường trong là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm $O$, góc \(45^{\circ}\) và phép vị tự tâm $O$, tỉ số \(\sqrt{2}\).
Bài giải:
♦ Cách 1:

Ta có \(OI=\sqrt{2}\).
Gọi $I’$ là ảnh của $I$ qua phép quay tâm $O$ góc \(45^o\) thì \(I'(0;\sqrt{2}).\)
Gọi \(I” \) là ảnh của \(I’\) qua phép vị tự tâm $O$ tỉ số \(\sqrt{2}\) thì \(I”=(0;2)\)
Đường tròn cần tìm có tâm \(I”\) bán kính bằng \(R=2\sqrt{2}.\)
Vậy phương trình đường tròn đó là: \(x^2+(y-2)^2=8\)
♦ Cách 2:
Gọi $(I’; R’)$ là ảnh của đường tròn(I; R) (R=2) qua phép quay \(Q_{(O,45^0)}\)
Ta có: \(\overrightarrow{OI}=(1;1),\overrightarrow{OI’}=(x’;y’)\)
Vì \(I’=Q_{(O,45^0)} (I)\) nên
\(\left\{ \begin{array}{l}
\cos {45^0} = \frac{{\overrightarrow {OI} .\overrightarrow {OI’} }}{{\left| {\overrightarrow {OI} } \right|.\left| {\overrightarrow {OI’} } \right|}}\\
\left| {\overrightarrow {OI} } \right| = \left| {\overrightarrow {OI’} } \right|
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
\frac{{x’ + y’}}{{\sqrt 2 .\sqrt {x{‘^2} + y{‘^2}} }} = \frac{{\sqrt 2 }}{2}\\
\sqrt 2 = \sqrt {x{‘^2} + y{‘^2}}
\end{array} \right.\)
\(\Leftrightarrow \left\{\begin{matrix} \sqrt{x’^2+y’^2}=x’+y’\\ \sqrt{x’^2+y’^2}=\sqrt{2} \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x’=0\\ y’=\sqrt{2} \end{matrix}\right.\) hoặc \(\Leftrightarrow \left\{\begin{matrix} x’=\sqrt{2}\\ y’= 0 \end{matrix}\right.\) nhưng góc quay dương nên \(I(O; \sqrt{2})\) và theo tính chất của phép quay thì $R’ = R = 2$.
Gọi $(I”; R”)$ là ảnh của $(I’; R’)$ qua phép vị tự \(V_{(O,\sqrt{2})}\), khi đó
\(I”=V_{(O,\sqrt{2})}(I’)\Leftrightarrow \overrightarrow{OI”}=\sqrt{2}\overrightarrow{OI’}\)
Mà \(\overrightarrow{OI”}=(x”, y”), \overrightarrow{OI’}=(0;\sqrt{2})\) nên \(\left\{\begin{matrix} x”=\sqrt{2.0}\\ y”=\sqrt{2}.\sqrt{2} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x” =0\\ y”=2 \end{matrix}\right.\)
⇔ $I”(0;2)$ và theo tính chất của phép vị tự thì \(R”=\sqrt{2}.R’=\sqrt{2}.2=2\sqrt{2}.\)
Vậy đường tròn $(I”)$ có phương trình: \(x^2+(y-2)^2=8\) là của đường tròn tâm $I(1;1)$ bán kính bằng $2$ qua phép đồng dạng nói trên.
4. Giải bài 4 trang 33 sgk Hình học 11
Cho tam giác $ABC$ vuông tại $A, AH$ là đường cao kẻ từ $A$. Tìm một phép đồng dạng biến tam giác $HBA$ thành tam giác $ABC$.
Bài giải:

Cho tam giác $ABC$ vuông cân tại $A, AH$ là đường cao kẻ từ $A$. Tìm một phép đồng dạng biến tam giác $HBA$ thành tam giác $ABC$.
Gọi $d$ là đường phân giác của góc $B$, xét đối xứng trục $Đd$ ta đó: A’ = Đd(A) $⇒ A’$ là giao điểm của đường thẳng đi qua $A$ với cạnh $BC, H’ $= Đd(H) $⇒ H’$ là giao điểm của đường thẳng đi qua $H$ với $AB.$
B = Đd(B), vậy \(\Delta H’BA’\) là ảnh của \(\Delta HBA\) qua phép đối xứng trục Đd.
Ta có \(\Delta HBA, \Delta ABC\) nên \(\Delta H’BA’ \sim \Delta ABC\) do đó:
\(\frac{AB}{H’B}=\frac{AC}{H’A’}=\frac{AC}{AH}\)
Xét phép vị tự \(V_{\left ( B, \frac{AC}{AH} \right )}\), ta có:
\(A=V_{\left ( B, \frac{AC}{AH} \right )}, (H’),C=V_{\left ( B, \frac{AC}{AH} \right )} (A’), B=V_{\left ( B, \frac{AC}{AH} \right )}(B)\)
Hay \(\Delta ABC\) là ảnh của \(\Delta HBA\) qua phép đồng dạng thu được từ việc thực hiện liên tiếp phép đối xứng qua đường phân giác của góc $B$ và phép vị tự tâm B, tỉ số \(\frac{AC}{AH}.\)
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 11 khác
- Để học tốt môn Vật lí lớp 11
- Để học tốt môn Sinh học lớp 11
- Để học tốt môn Ngữ văn lớp 11
- Để học tốt môn Lịch sử lớp 11
- Để học tốt môn Địa lí lớp 11
- Để học tốt môn Tiếng Anh lớp 11
- Để học tốt môn Tiếng Anh lớp 11 thí điểm
- Để học tốt môn Tin học lớp 11
- Để học tốt môn GDCD lớp 11
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 11 với giải bài 1 2 3 4 trang 33 sgk Hình học 11!
“Bài tập nào khó đã có giaibaisgk.com“
