Hướng dẫn Giải bài 32 33 34 35 36 trang 128 129 sgk Toán 8 tập 1

Nội Dung

Hướng dẫn giải Bài §5. Diện tích hình thoi, chương II – Đa giác. Diện tích đa giác, sách giáo khoa toán 8 tập một. Nội dung bài giải bài 32 33 34 35 36 trang 128 129 sgk toán 8 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 8.

Lý thuyết

1. Cách tính diện tích của một tứ giác có hai đường chéo vuông góc

Cho tứ giác ABCD có $AC \bot B{\rm{D}}$, AC=6cm; BD=7cm. Tính diện tích ABCD.

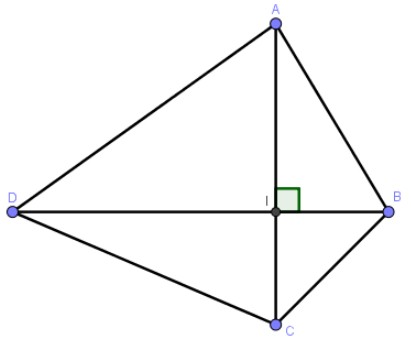
Bài giải:

Gọi I là giao điểm của hai đường chéo.

Ta có:

$\begin{array}{l} {S_{ABCD}} = {S_{ABD}} + {S_{BC{\rm{D}}}}\\ = \frac{1}{2}AI.BD + \frac{1}{2}IC.BD\\ = \frac{1}{2}BD.\left( {AI + IC} \right)\\ = \frac{1}{2}B{\rm{D}}.AC = \frac{1}{2}.6.7 = 21(c{m^2}) \end{array}$

Nhận xét: Diện tích của một tứ giác có hai đường chéo vuông góc bằng một nửa tích hai đường chéo.

2. Công thức tính diện tích hình thoi

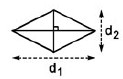
Diện tích hình thoi bằng nửa tích hai đường chéo

$S = \frac{1}{2}{d_1}.{d_2}$

Lưu ý: Hình thoi cũng là một hình bình hành đặc biệt nên ta có thể sử dụng công thức tính diện tích hình bình hành để tính diện tích hình thoi.

Dưới đây là phần Hướng dẫn trả lời các câu hỏi có trong bài học cho các bạn tham khảo. Các bạn hãy đọc kỹ câu hỏi trước khi trả lời nhé!

Câu hỏi

1. Trả lời câu hỏi 1 trang 127 sgk Toán 8 tập 1

Hãy tính diện tích tứ giác $ABCD$ theo $AC, BD$, biết $AC ⊥ BD$ tại $H$ (h.$145$)

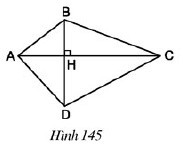
Trả lời:

Ta có:

${S_{ABC}} = \dfrac{1}{2}BH.AC$

${S_{ADC}}=\dfrac{1}{2}DH.AC$

${S_{ABCD}} = {S_{ABC}} + {S_{ADC}}$$ \,= \dfrac{1}{2}BH.AC + \dfrac{1}{2}DH.AC$$\, = \dfrac{1}{2}(BH + DH).AC = \dfrac{1}{2}BD.AC$

2. Trả lời câu hỏi 2 trang 127 sgk Toán 8 tập 1

Hãy viết công thức tính diện tích hình thoi theo hai đường chéo.

Trả lời:

Hình thoi có độ dài hai đường chéo lần lượt là $d_1 ,d_2$.

Diện tích hình thoi là: $S = \dfrac{1}{2}{d_1}{d_2}$.

3. Trả lời câu hỏi 3 trang 127 sgk Toán 8 tập 1

Hãy tính diện tích hình thoi bằng cách khác.

Trả lời:

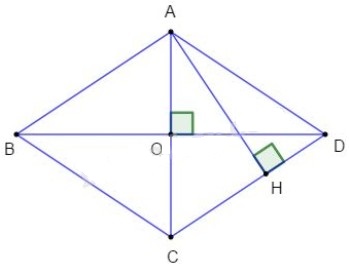
Hình thoi $ABCD$ cũng là hình bình hành.

Kẻ đường cao $AH $ ứng với $CD$.

$⇒{S_{ABCD}} = AH.CD = 2{S_{ACD}}$

Tam giác $ACD$ có đường cao $DO$ ứng với cạnh $AC$.

$ \Rightarrow {S_{ACD}} = \dfrac{1}{2}DO.AC$

Do đó:

${S_{ABCD}} = 2{S_{ACD}} = 2.\dfrac{1}{2}.DO.AC $$\,= \dfrac{1}{2}.\left( {2DO} \right).AC = \dfrac{1}{2}.BD.AC$

($O$ là trung điểm $BD$ nên $BD = 2DO$).

Dưới đây là Hướng dẫn giải bài 32 33 34 35 36 trang 128 129 sgk toán 8 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 8 kèm bài giải chi tiết bài 32 33 34 35 36 trang 128 129 sgk toán 8 tập 1 của bài §5. Diện tích hình thoi trong chương II – Đa giác. Diện tích đa giác cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 32 33 34 35 36 trang 128 129 sgk toán 8 tập 1

1. Giải bài 32 trang 128 sgk Toán 8 tập 1

a) Hãy vẽ một tứ giác có độ dài hai đường chéo là 3,6cm, 6cm và hai đường chéo đó vuông góc với nhau. Có thể vẽ được bao nhiêu tứ giác như vậy? Hãy tính diện tích mỗi tứ giác vừa vẽ?

b) Hãy tính diện tích hình vuông có độ dài đường chéo là d.

Bài giải:

a) Ta có hình vẽ sau:

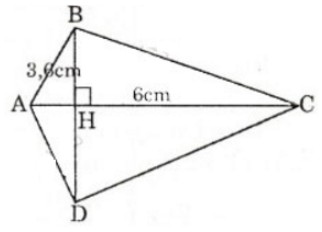
Ta vẽ được tứ giác ABCD có đường chéo AC = 6cm, BD = 3,6cm, AC vuông góc với BD

Gọi H là giao điểm của AC và BD ⇒ H di chuyển trên đoạn AC

⇒ Vẽ được vô số tứ giác như tứ giác ABCD.

Diện tích của tứ giác ABCD là:

S_ABCD= $\frac{1}{2}$ AC. BD = $\frac{1}{2}$ 6. 3,6 = 10,8 (cm²)

b) Hình vuông cũng là hình thoi ⇒ Diện tích hình vuông có độ dài đường chéo là d

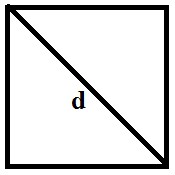
S = $\frac{1}{2}$ d.d = $\frac{1}{2}$ d²

2. Giải bài 33 trang 128 sgk Toán 8 tập 1

Vẽ hình chữ nhật có một cạnh bằng đường chéo của một hình thoi cho trước và có diện tích bằng diện tích của hình thoi đó. Từ đó suy ra cách tính diện tích hình thoi.

Bài giải:

Ta có hình vẽ sau:

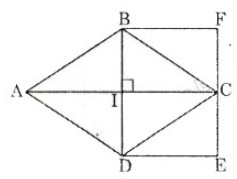
Cho hình thoi ABCD, vẽ hình chữ nhật có một cạnh là đường chéo BD, cạnh còn lại là cạnh FE (IC = $\frac{1}{2}$ AC).

Khi đó diện tích của hình chữ nhật BFED bằng diện tích hình thoi ABCD.

S_BFED = BD. IC = BD. $\frac{1}{2}$ AC = S_ABCD

3. Giải bài 34 trang 128 sgk Toán 8 tập 1

Cho một hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật . Vì sao tứ giác này là một hình thoi? So sánh diện tích hình thoi và diện tích hình chữ nhật, từ đó suy ra cách tính diện tích hình thoi.

Bài giải:

Giả sử ta có hình chữ nhật ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

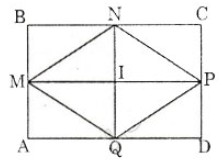
Do ABCD là hình chữ nhật ⇒ BC = AD và AB = CD

⇒ Mặt khác ta có M, N là trung điểm của AB và BC

⇒ BN = MA và AQ = BN

⇒ ∆AMQ = ∆BNM (góc cạnh góc)

⇒ MN = MQ

Chứng minh tương tự ta được: MN = NP ; NP = QP

⇒ MN = NP = MQ = QP

⇒ Tứ giác MNPQ là hình thoi

Diện tích tứ giác MNPQ là:

S_MNPQ = $\frac{1}{2}$ MP. NQ

mà S_ABCD= AB. AD = MP. NQ

⇒ S_MNPQ = $\frac{1}{2}$ MP.NQ

⇒ S_MNPQ = $\frac{1}{2}$ S_ABCD

4. Giải bài 35 trang 129 sgk Toán 8 tập 1

Tính diện tích hình thoi có cạnh dài $6cm$ và một trong các góc của nó có số đo là $60^{\circ}$

Bài giải:

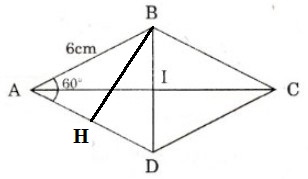
Giả sử hình thoi ABCD có cạnh AB = 6cm, $\widehat{A}$ = $60^{\circ}$

Do ABCD là hình thoi ⇒ AB = AD mà $\widehat{A}$ = $60^{\circ}$ ⇒ ∆ABC là tam giác đều

Từ B vẽ BH $\perp$ AD ⇒ HA = HD (Do ∆ABC là tam giác đều).

Áp dụng định lý Py-ta-go vào tam giác vuông BHD.

BH² = AB² – AH² = AB² – $\left ( \frac{AB}{2} \right )^{2}$

= AB² – $\frac{AB^{2}}{4}$ = $\frac{3AB^{2}}{4}$.

⇒ BH = $\frac{6\sqrt{3}}{2}$ = 3√ 3 (cm)

Diện tích hình thoi là:

S_ABCD= BH. AD = 3√ 3. 6 = 18√ 3 (cm²)

5. Giải bài 36 trang 129 sgk Toán 8 tập 1

Cho một hình thoi và một hình vuông có cùng chu vi. Hỏi hình nào có diện tích lớn hơn? Vì sao?

Bài giải:

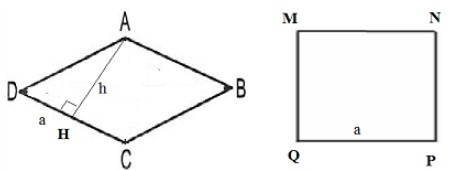
Giả sử hình thoi ABCD và hình vuông MNPQ có cùng chu vi là 4a.

⇒ Độ dài của cạnh hình vuông = hình thoi = $a$

Ta có diện tích hình vuông MNPQ: S_MNPQ = a²

Từ đỉnh góc tù A của hình thoi ABCD vẽ đường cao AH có độ dài $h$.

⇒ Diện tích hình thoi ABCD: S_ABCD= $ah$

Mặt khác h ≤ a (đường vuông góc nhỏ hơn đường xiên) nên ah ≤ a²

Vậy S_ABCD≤ S_MNPQ

Dấu $“=”$ xảy ra khi $h = a$ hay $H$ trùng với $D$, nghĩa là hình thoi $ABCD$ trở thành hình vuông.

Bài trước:

Giải bài 26 27 28 29 30 31 trang 125 126 sgk Toán 8 tập 1

Bài tiếp theo:

Giải bài 37 38 39 40 trang 130 131 sgk Toán 8 tập 1

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 8 với giải bài 32 33 34 35 36 trang 128 129 sgk toán 8 tập 1!

“Bài tập nào khó đã có giaibaisgk.com“