Nội Dung
Hướng dẫn giải Bài §6. Trường hợp đồng dạng thứ hai, Chương III – Tam giác đồng dạng, sách giáo khoa toán 8 tập hai. Nội dung bài giải bài 32 33 34 trang 77 sgk toán 8 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 8.
Lý thuyết
Định lí
Nếu hai cạnh tam giác nảy tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi hai cặp cạch đó bằng nhau, thì hai tam giác đồng dạng.
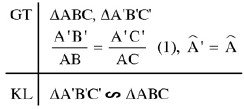
Tam giác ABC và tam giác DEF có: $\frac{AB}{AC}=\frac{DE}{EF}$ (do $\frac{4}{3}=\frac{8}{6}$) và $\widehat{BAC}=\widehat{EDF}$
⇒ $\Delta ABC \sim \Delta DEF$
Dưới đây là phần Hướng dẫn trả lời các câu hỏi có trong bài học cho các bạn tham khảo. Các bạn hãy đọc kỹ câu hỏi trước khi trả lời nhé!
Câu hỏi
1. Trả lời câu hỏi 1 trang 75 sgk Toán 8 tập 2
Cho hai tam giác \(ABC\) và \(DEF\) có kích thước như trong hình 36.
– So sánh các tỉ số \(\dfrac{{AB}}{{DE}}\) và \( \dfrac{{AC}}{{DF}}\)
– Đo các đoạn thẳng \(BC, EF\). Tính tỉ số \(\dfrac{{BC}}{{EF}}\), so sánh với các tỉ số trên và dự đoán sự đồng dạng của hai tam giác \(ABC\) và \(DEF.\)

Trả lời:
Ta có:
\(\dfrac{{AB}}{{DE}} = \dfrac{{AC}}{{DF}} = \dfrac{1}{2}\)
Đo các cạnh ta có: \(BC = \,6 ; EF = 12 \)
\(\eqalign{& \Rightarrow {{BC} \over {EF}} = {1 \over 2} \cr & \Rightarrow {{AB} \over {DE}} = {{AC} \over {DF}} = {{BC} \over {EF}} = {1 \over 2} \cr} \)
Dự đoán: \(ΔABC\) đồng dạng \(ΔDEF\).
2. Trả lời câu hỏi 2 trang 76 sgk Toán 8 tập 2
Hãy chỉ ra các cặp tam giác đồng dạng với nhau từ các tam giác sau đây (h.38):

Trả lời:
Xét \(ΔABC\) và \(ΔDEF\) có:
\(\eqalign{& \widehat A = \widehat D = {70^o} \cr & {{AB} \over {AC}} = {{DE} \over {DF}} = {2 \over 3} \cr} \)
\(⇒ ΔABC\) đồng dạng \(ΔDEF\) (c.g.c)
3. Trả lời câu hỏi 3 trang 77 sgk Toán 8 tập 2
a) Vẽ tam giác \(ABC\) có \(\widehat {BAC} = {50^o}\), \(AB = 5cm, AC = 7,5cm\) (h.39)
b) Lấy trên các cạnh \(AB, AC\) lần lượt hai điểm \(D, E\) sao cho \(AD = 3cm, AE = 2cm\). Hai tam giác \(AED\) và \(ABC\) có đồng dạng với nhau không ? Vì sao ?

Trả lời:
Ta có:
\(\dfrac{{AB}}{{AC}} = \dfrac{5}{{7,5}} = \dfrac{2}{3}\)
\(\dfrac{{AE}}{{AD}} = \dfrac{2}{3}\)
Xét \(\Delta ABC\) và \(\Delta AED\) có
\(\widehat A\) chung
\(\dfrac{{AB}}{{AC}} = \dfrac{{AE}}{{AD}} = \dfrac{2}{3}\)
\( \Rightarrow \Delta ABC\) đồng dạng \( \Delta AED\,\,\left( {c.g.c} \right) \)
Dưới đây là Hướng dẫn giải bài 32 33 34 trang 77 sgk toán 8 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 8 kèm bài giải chi tiết bài 32 33 34 trang 77 sgk toán 8 tập 2 của Bài §6. Trường hợp đồng dạng thứ hai trong Chương III – Tam giác đồng dạng cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 32 trang 77 sgk Toán 8 tập 2
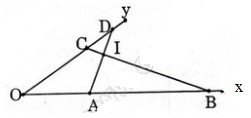
Trên một cạnh của góc \(xOy\) (\(\widehat{xOy}=180^0\)). Đặt các đoạn thẳng \(OA= 5cm, OB= 16cm\). Trên cạnh thứ hai của góc đó, đặt các đoạn \(OC= 8cm, OD= 10cm\).
a) Chứng minh hai tam giác \(OCB\) và \(OAD\) đồng dạng.
b) Gọi giao điểm của các cạnh \(AD\) và \(BC\) là \(I\), chứng minh rằng hai tam giác \(IAB\) và \(ICD\) có góc các góc bằng nhau từng đôi một.
Bài giải:
a) \(\frac{OA}{OC}= \frac{5}{8} ; \frac{OD}{OB}= \frac{10}{16} = \frac{5}{8}\)
\(\Rightarrow \frac{OA}{OC}= \frac{OD}{OB}\)
Xét \(∆OCB\) và \(∆OAD\) có:
\(\widehat O\) chung
\(\frac{OA}{OC}\) = \(\frac{OD}{OB}\)
\(\Rightarrow ∆OCB ∽ ∆OAD\) (trường hợp đồng dạng thứ 2)
\(\Rightarrow \widehat {ODA} = \widehat {CBO}\) hay \(\widehat{CDI}= \widehat{IBA}\)
b) \(∆ICD\) và \(∆IAI\) có:
\(\widehat{CID}= \widehat{AIB}\) (hai góc đối đỉnh) (1)
\(\widehat{CDI}= \widehat{IBA}\) (theo câu a) (2)
Theo định lí tổng ba góc trong một tam giác ta có:
\(\eqalign{& \widehat {CID} + \widehat {CDI} + \widehat {ICD} = {180^0} \cr & \widehat {AID} + \widehat {IBA} + \widehat {IAB} = {180^0} \cr} \)
\( \Rightarrow \widehat {CID} + \widehat {CDI} + \widehat {ICD} = \widehat {AID} + \widehat {IBA} + \widehat {IAB}\) (3)
Từ (1), (2) và (3) suy ra: \( \widehat {ICD}=\widehat {IAB}\).
Vậy hai tam giác $\Delta IAB;\,\ \Delta ICD$ có các góc bằng nhau từng đôi một.
2. Giải bài 33 trang 77 sgk Toán 8 tập 2
Chứng minh rằng nếu tam giác \(A’B’C’\) đồng dạng với tam giác \(ABC\) theo tỉ số \(k\), thì tỉ số của hai đường trung tuyến tương ứng với hai tam giác đó cũng bằng \(k\).
Bài giải:

Giả sử \(∆A’B’C’\) đồng dạng \(∆ABC\) theo tỉ số \(k, AM, A’M’\) là hai đường trung tuyến tương ứng.
Vì \(∆A’B’C’\) đồng dạng \(∆ABC\) (giả thiết)
\(\dfrac{A’B’}{AB} = \dfrac{B’C’}{BC}\) (tính chất hai tam giác đồng dạng)
Mà \(B’C’ = 2B’M’, BC = 2BM\) (tính chất trung tuyến)
\( \Rightarrow \dfrac{{A’B’}}{{AB}} = \dfrac{{2B’M’}}{{2BM}} = \dfrac{{B’M’}}{{BM}}\)
Xét \(∆ABM\) và \( ∆A’B’M’\) có:
\(\widehat{B} = \widehat{B’}\) (vì \(∆A’B’C’\) đồng dạng \(∆ABC\))
\( \dfrac{{A’B’}}{{AB}} = \dfrac{{B’M’}}{{BM}}\) (chứng minh trên)
\( \Rightarrow ∆A’B’M’ \) đồng dạng \(∆ABM\) (c-g-c)
\( \Rightarrow \dfrac{A’M’}{AM}= \dfrac{A’B’}{AB} = k.\)
3. Giải bài 34 trang 77 sgk Toán 8 tập 2
Dựng tam giác \(ABC\), biết \(\widehat{A}={60^o}\) và, tỉ số \(\dfrac{AB}{AC} = \dfrac{4}{5}\) và đường cao \(AH = 6cm\).
Bài giải:
♦ Dựng hình

– Dựng \(\widehat {xAy} = {60^o}\)
– Trên hai cạnh \(Ax, Ay\) của góc \(\widehat{xAy}\) lần lượt dựng \(AM = 4\,cm\), \(AN = 5\,cm\). Kẻ đường cao \(AI\) của \(∆AMN\).
– Trên tia \(AI\) lấy điểm \(H\) sao cho \(AH = 6\,cm\), qua \(H\) vẽ đường song song với \(MN\) cắt \(Ax, Ay\) lần lượt tại \(B\) và \(C\)
\( \Rightarrow \) \(∆ABC\) thỏa mãn điều kiện bài toán.
♦ Chứng minh:
Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho ta có:
\(MN // BC\) (theo cách dựng)
Suy ra \(∆AMN\) đồng dạng \(∆ABC\).
\( \Rightarrow \dfrac{AM}{AN} = \dfrac{AB}{AC} = \dfrac{4}{5}\) (tính chất hai tam giác đồng dạng)
Vì \(AH ⊥ MN\), mà \(MN//BC\) nên \(AH\bot BC\), \(AH = 6\,cm\) \( \Rightarrow \) \(AH\) là đường cao của tam giác \(ABC\).
Vậy tam giác \(ABC\) thỏa mãn yêu cầu bài toán.
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 8 khác
- Để học tốt môn Vật lí lớp 8
- Để học tốt môn Sinh học lớp 8
- Để học tốt môn Ngữ văn lớp 8
- Để học tốt môn Lịch sử lớp 8
- Để học tốt môn Địa lí lớp 8
- Để học tốt môn Tiếng Anh lớp 8
- Để học tốt môn Tiếng Anh lớp 8 thí điểm
- Để học tốt môn Tin học lớp 8
- Để học tốt môn GDCD lớp 8
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 8 với giải bài 32 33 34 trang 77 sgk toán 8 tập 2!
“Bài tập nào khó đã có giaibaisgk.com“
