Nội Dung
Hướng dẫn giải Bài §7. Trường hợp đồng dạng thứ ba, Chương III – Tam giác đồng dạng, sách giáo khoa toán 8 tập hai. Nội dung bài giải bài 35 36 37 trang 79 sgk toán 8 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 8.
Lý thuyết
Định lí
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
$\Delta ABC$ và $\Delta A’B’C’$ có: $\widehat{A}=\widehat{A’};\,\ \widehat{B}=\widehat{B’}$
⇒ $\Delta ABC \sim \Delta A’B’C’$ (trường hợp góc – góc)
Dưới đây là phần Hướng dẫn trả lời các câu hỏi có trong bài học cho các bạn tham khảo. Các bạn hãy đọc kỹ câu hỏi trước khi trả lời nhé!
Câu hỏi
1. Trả lời câu hỏi 1 trang 78 sgk Toán 8 tập 2
Trong các tam giác dưới đây, những cặp tam giác nào đồng dạng với nhau ? Hãy giải thích (h.41)
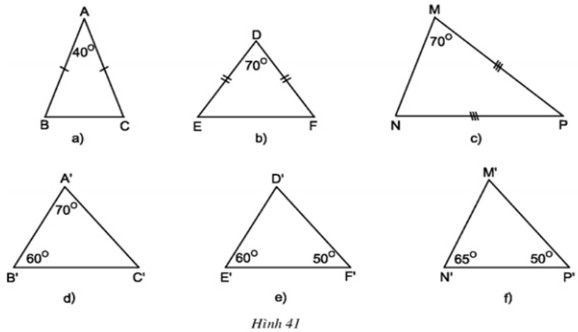
Trả lời:
\(ΔABC\) có \(\widehat A + \widehat B + \widehat C = {180^o}\)
Mà \(ΔABC\) cân tại \(A \Rightarrow \widehat B = \widehat C\)
\( \Rightarrow \widehat B + \widehat C = {180^o} – \widehat A\)
\(\Rightarrow \widehat B = \widehat C = \dfrac{{\left( {{{180}^o} – {{40}^o}} \right)}}{2} = {70^o}\)
\(ΔMNP\) cân tại \(P \Rightarrow \widehat M = \widehat N = {70^o}\)
\(ΔABC\) và \(ΔPMN\) có
\(\eqalign{& \widehat B = \widehat M = {70^o} \cr & \widehat C = \widehat N = {70^o} \cr & \Rightarrow \Delta ABC \text{ đồng dạng } \Delta PMN\,\,\left( {g.g} \right) \cr} \)
\(\Delta A’B’C’\) có \(\widehat {A’} + \widehat {B’} + \widehat {C’} = {180^o}\)
\( \Rightarrow \widehat {C’} = {180^o} – \left( {\widehat {A’} + \widehat {B’}} \right) \)\(\,= {180^o} – \left( {{{70}^o} + {{60}^o}} \right) = {50^o}\)
\(ΔA’B’C’\) và \(ΔD’E’F’\) có
\(\eqalign{& \widehat {B’} = \widehat {E’} = {60^o} \cr & \widehat {C’} = \widehat {F’} = {50^o} \cr & \Rightarrow \Delta A’B’C’ \text{ đồng dạng } \Delta D’E’F’\,\,\left( {g.g} \right) \cr} \)
2. Trả lời câu hỏi 2 trang 79 sgk Toán 8 tập 2
Ở hình 42 cho biết \(AB = 3cm\); \(AC = 4,5cm\) và \(\widehat {ABD} = \widehat {BCA}\)
a) Trong hình vẽ này có bao nhiêu tam giác ? Có cặp tam giác nào đồng dạng với nhau không ?
b) Hãy tính các độ dài \(x\) và \(y\) (\(AD = x, DC = y\)).
c) Cho biết thêm \(BD\) là tia phân giác của góc \(B\). Hãy tính độ dài các đoạn thẳng \(BC\) và \(BD\).
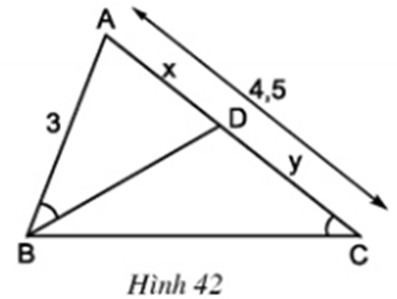
Trả lời:
a) Trong hình vẽ có \(3\) tam giác: \(ΔABD, ΔCBD, ΔABC\).
\(ΔABD\) và \(ΔACB\) có
\(\widehat B = \widehat C\)
\(\widehat A\) chung
\(⇒ ΔABD\) đồng dạng \(ΔACB\) (g.g)
b) \(ΔABD\) đồng dạng \(ΔACB\)
\(\eqalign{& \Rightarrow {{AB} \over {AD}} = {{AC} \over {AB}} \Rightarrow {3 \over {AD}} = {{4,5} \over 3} \cr & \Rightarrow AD = x = {{3.3} \over {4,5}} = 2 \cr} \)
\(⇒ y = 4,5 – 2 = 2,5\)
c) \(BD\) là tia phân giác của góc \(B\).
\(\eqalign{ & \Rightarrow {{AB} \over {BC}} = {x \over y} \Rightarrow {3 \over {BC}} = {2 \over {2,5}} \cr & \Rightarrow BC = {{3.2,5} \over 2} = 3,75 \cr} \)
Ta có: \(\eqalign{& \Delta ABD \text{ đồng dạng }\Delta ACB \cr & \Rightarrow {{AB} \over {BD}} = {{AC} \over {BC}} \Rightarrow {3 \over {BD}} = {{4,5} \over {3,75}} \cr & \Rightarrow BD = {{3.3,75} \over {4,5}} = 2,5 \cr} \)
Dưới đây là Hướng dẫn giải bài 35 36 37 trang 79 sgk toán 8 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 8 kèm bài giải chi tiết bài 35 36 37 trang 79 sgk toán 8 tập 2 của Bài §7. Trường hợp đồng dạng thứ ba trong Chương III – Tam giác đồng dạng cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
1. Giải bài 35 trang 79 sgk Toán 8 tập 2
Chứng minh rằng nếu tam giác \(A’B’C’\) đồng dạng với tam giác \(ABC\) theo tỉ số \(k\) thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng \(k\).
Bài giải:
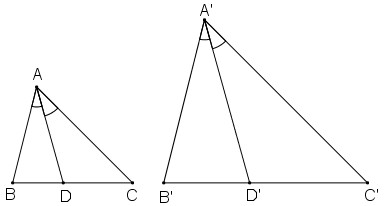
\(∆A’B’C’ ∽ ∆ABC\) theo tỉ số \(k= \dfrac{A’B’}{AB}\)
\(AD, A’D’\) lần lượt là đường phân giác của hai tam giác \(ABC;\,A’B’C’\)
\( \Rightarrow \widehat {BAC} = \widehat {B’A’C’}\) (1) (tính chất hai tam giác đồng dạng)
\(AD\) là phân giác góc \(\widehat {BAC}\) (gt)
\( \Rightarrow\) \(\widehat {BAD} = \dfrac{1}{2}\widehat {BAC}\) (2) (tính chất tia phân giác)
\(A’D’\) là phân giác góc \(\widehat {B’A’C’}\) (gt)
\( \Rightarrow\) \(\widehat {B’A’D’} =\dfrac{1}{2}\widehat {B’A’C’}\) (3) (tính chất tia phân giác)
Từ \((1),(2)\) và \((3)\) suy ra: \(\widehat{BAD}\) = \(\widehat{B’A’D’}\)
Xét \(∆A’B’D’\) và \(∆ABD\) có:
+) \(\widehat{B}\) = \(\widehat{B’}\) (vì \(∆A’B’C’ ∽ ∆ABC\))
+) \(\widehat{BAD}\) = \(\widehat{B’A’D’}\) (chứng minh trên)
\(\Rightarrow ∆A’B’D’ ∽ ∆ABD\) (g-g)
\( \Rightarrow \dfrac{A’B’}{AB}= \dfrac{A’D’}{AD}=k\)
2. Giải bài 36 trang 79 sgk Toán 8 tập 2
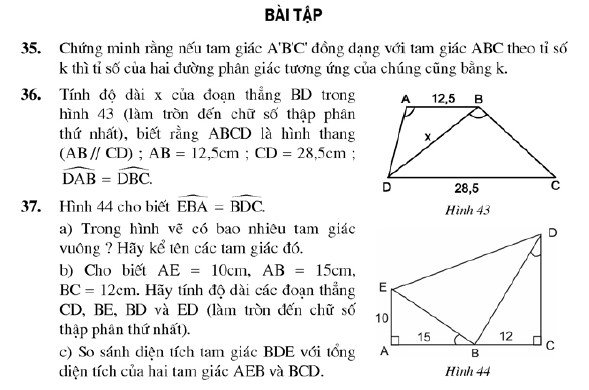
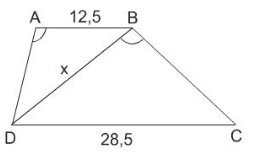
Tính độ dài \(x\) của đoạn thẳng \(BD\) trong hình 43 (Làm tròn đến chữ thập phân thứ nhất), biết rằng \(ABCD\) là hình thang (\(AB // CD\)); \(AB= 12,5cm; CD= 28,5cm\)
\(\widehat{DAB} = \widehat{DBC}\).
Bài giải:
Xét \(∆ABD\) và \(∆BDC\) có:
+) \(\widehat{DAB}\) = \(\widehat{DBC}\) (giả thiết)
+) \(\widehat{ABD}\) = \(\widehat{BDC}\) (Hai góc so le trong)
\( \Rightarrow ∆ABD ∽ ∆BDC\) (g-g)
\( \Rightarrow \dfrac{AB}{BD} = \dfrac{BD}{DC}\) (tính chất hai tam giác đồng dạng)
\( \Rightarrow B{D^2} = AB.DC\)
\( \Rightarrow BD = \sqrt {AB.DC} = \sqrt {12,5.28,5} \) \( \approx 18,87 cm\)
3. Giải bài 37 trang 79 sgk Toán 8 tập 2
Hình 44 cho biết \(\widehat{EBA} = \widehat{BDC}\).
a) Trong hình vẽ, có bao nhiêu tam giác vuông? Hãy kể tên các tam giác đó.
b) Cho biết \(AE = 10cm, AB = 15cm, BC = 12cm\). Hãy tính độ dài các đoạn thẳng \(CD, BE, BD\) và \(ED\) (làm tròn đến chữ số thập phân thứ nhất).
c) So sánh diện tích tam giác \(BDE\) với tổng diện tích hai tam giác \(AEB\) và \(BCD\).

Bài giải:
a) Ta có: \(\widehat{EBA} = \widehat{BDC}\) (giả thiết) mà \(\widehat{BDC} + \widehat{CBD}={90^0}\)
\( \Rightarrow \widehat{EBA} + \widehat{CBD}={90^0}\)
Vậy \(\widehat{EBD} = {180^0} – (\widehat{EBA}+ \widehat{CBD})\)\(\, = {180^o} – {90^o} = {90^o}\)
Vậy trong hình vẽ có ba tam giác vuông đó là:
\(∆ABE, ∆CBD, ∆EBD.\)
b) \(∆ABE\) và \(∆CDB\) có:
\(\widehat{A} = \widehat{C}=90^o\)
\(\widehat{ABE}= \widehat{CDB}\) (giả thiết)
\( \Rightarrow ∆ABE ∽ ∆CDB\) (g-g)
\( \Rightarrow \dfrac{AB}{CD} = \dfrac{AE}{CB}\) (tính chất hai tam giác đồng dạng)
\( \Rightarrow CD = \dfrac{AB.CB}{AE} = 18\, (cm)\)
Áp dụng định lí pitago ta có:
\( ∆ABE\) vuông tại \(A\)
\( \Rightarrow BE = \sqrt{AE^{2}+AB^{2}}\) \(\,=\sqrt{10^{2}+15^{2}}\) \( \approx 18\, (cm)\).
\(∆BCD\) vuông tại \(C\)
\( \Rightarrow BD = \sqrt {B{C^2} + D{C^2}} \) \(= \sqrt {{{12}^2} + {{18}^2}} \approx 21,6\,\,cm\)
\(∆EBD\) vuông tại \(B\)
\( \Rightarrow ED = \sqrt{EB^{2}+BD^{2}}\) \(=\sqrt{325+ 468} \approx 28,2\, (cm)\)
c) Ta có:
\(S_{ABE} + S_{DBC}\)
\(= \dfrac{1}{2}AE.AB + \dfrac{1}{2}BC.CD\)
\(= \dfrac{1}{2}. 10.15 + \dfrac{1}{2}.12.18\)
\(= 75 + 108 = 183\;cm^2\).
Ta có: \(A{\rm{E}}//DC\,\,\left(\text{ cùng } { \bot AC} \right) \Rightarrow \) \(ACDE\) là hình thang.
\(S_{ACDE} = \dfrac{1}{2}.(AE + CD).AC\)
\(= \dfrac{1}{2}.(10 + 18).27= 378\;cm^2\)
\( \Rightarrow S_{EBD} = S_{ACDE} – (S_{ABE}+ S_{DBC})\)\(\; = 378 – 183 = 195\,cm^2\)
\(S_{EBD}> S_{ABE} + S_{DBC}\) \(( 195 > 183)\).
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 8 khác
- Để học tốt môn Vật lí lớp 8
- Để học tốt môn Sinh học lớp 8
- Để học tốt môn Ngữ văn lớp 8
- Để học tốt môn Lịch sử lớp 8
- Để học tốt môn Địa lí lớp 8
- Để học tốt môn Tiếng Anh lớp 8
- Để học tốt môn Tiếng Anh lớp 8 thí điểm
- Để học tốt môn Tin học lớp 8
- Để học tốt môn GDCD lớp 8
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 8 với giải bài 35 36 37 trang 79 sgk toán 8 tập 2!
“Bài tập nào khó đã có giaibaisgk.com“
