Hướng dẫn Giải bài 33 34 35 trang 123 sgk Toán 7 tập 1

Nội Dung

Hướng dẫn giải Bài §5. Trường hợp bằng nhau thứ ba của tam giác góc – cạnh – góc (g.c.g), chương II – Tam giác, sách giáo khoa toán 7 tập một. Nội dung bài giải bài 33 34 35 trang 123 sgk toán 7 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 7.

Lý thuyết

1. Vẽ tam giác biết một cạnh và hai góc kề

Để vẽ được tam giác ABC tổng các số đo của hai góc đã cho phải nhỏ hơn ${180^0}$

2. Trường hợp bằng nhau góc – cạnh – góc

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

3. Hệ quả

Hệ quả 1:

Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì tam giác vuông đó bằng nhau.

Hệ quả 2:

Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì tam giác vuông đó bằng nhau.

Dưới đây là phần Hướng dẫn trả lời các câu hỏi có trong bài học cho các bạn tham khảo. Các bạn hãy đọc kỹ câu hỏi trước khi trả lời nhé!

Câu hỏi

1. Trả lời câu hỏi 1 trang 121 sgk Toán 7 tập 1

Vẽ thêm tam giác $A’B’C’$ có: $B’C’ = 4cm;\;\widehat {B’} = {60^o};\,\,\widehat {C’} = {40^o}$. Hãy đo để kiểm nghiệm rằng $AB = A’B’.$ Vì sao ta kết luận được $ΔABC = ΔA’B’C’$?

Trả lời:

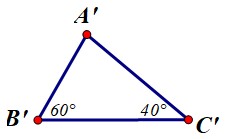
Đo kiểm tra thấy: $AB=A’B’$

$ΔABC$ và $ΔA’B’C’$ có:

+) $AB = A’B’$ (chứng minh trên)

+) $\widehat B = \widehat {B’}=60^o$

+) $BC = B’C’=4\,cm$

Suy ra $ΔABC = ΔA’B’C’$ (cạnh – góc – cạnh).

2. Trả lời câu hỏi 2 trang 122 sgk Toán 7 tập 1

Tìm các tam giác bằng nhau ở mỗi hình 94, 95, 96.

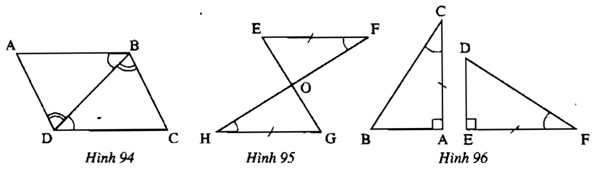
Trả lời:

– Hình 94: Xét $ΔABD$ và $ΔCDB$ có:

+) $\widehat {ABD} = \widehat {CDB}\,\,\left( {gt} \right)$

+) $BD$ cạnh chung

+) $\widehat {ADB} = \widehat {CBD}\,(gt)$

$ \Rightarrow ΔABD = ΔCDB$ (g.c.g)

– Hình 95: Áp dụng định lí tổng các góc của một tam giác vào $\Delta OEF$ và $\Delta OHG$ ta có:

$\widehat {EOF} + \widehat {OFE} + \widehat {FEO} = {180^o}$ (1)

$\widehat {GOH} + \widehat {OHG} + \widehat {HGO} = {180^o}$ (2)

$\widehat {EOF} = \widehat {GOH}$ (đối đỉnh) (3)

$\widehat {OFE} = \widehat {OHG}$ (giả thiết) (4)

Từ (1), (2), (3), (4) ta có: $\widehat {FEO} = \widehat {HGO}$

Xét $ΔEOF$ và $ΔGOH$ có:

+) $\widehat {OFE} = \widehat {OHG}$ (giả thiết)

+) $EF = GH$ (giả thiết)

+) $\widehat {FEO} = \widehat {HGO}$ (chứng minh trên)

$ \Rightarrow ΔEOF = ΔGOH$ (g.c.g)

– Hình 96: Xét $ΔABC$ và $ΔEDF$ có:

+) $\widehat {BAC} = \widehat {DEF}=90^o$

+) $AC = EF$ (giả thiết)

+) $\widehat {ACB} = \widehat {EFD}$ (giả thiết)

$\Rightarrow ΔABC = ΔEDF$ (g.c.g)

Dưới đây là Hướng dẫn giải bài 33 34 35 trang 123 sgk toán 7 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 7 kèm bài giải chi tiết bài 33 34 35 trang 123 sgk toán 7 tập 1 của bài §5. Trường hợp bằng nhau thứ ba của tam giác góc – cạnh – góc (g.c.g) trong chương II – Tam giác cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 33 34 35 trang 123 sgk toán 7 tập 1

1. Giải bài 33 trang 123 sgk Toán 7 tập 1

Vẽ tam giác $ABC$ biết $AC = 2cm$, $\widehat{A}$ = $90^0$, $\widehat{C}$ = $60^0$.

Bài giải:

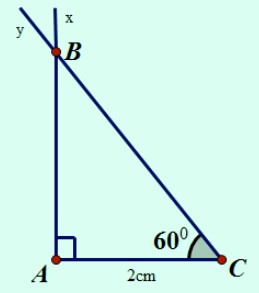
– Vẽ đoạn thẳng $AC$.

– Trên cùng một nửa mặt phẳng bờ $AC$, vẽ tia $Ax$ sao cho $\widehat{CAx}$ = $90^0$, vẽ tia $Cy$ sao cho $\widehat{ACy}$ = $60^0$.

– Hai tia $Ax$ và $By$ cắt nhau tại $B$. Tam giác $ABC$ là tam giác cần vẽ.

2. Giải bài 34 trang 123 sgk Toán 7 tập 1

Trên mỗi hình 98, 99 có các tam giác nào bằng nhau? Vì sao?

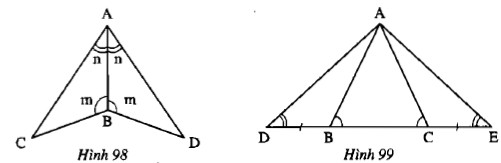
Bài giải:

– Hình 98: Xét hai tam giác BCA và BDA có:

$\left.\begin{matrix} \widehat{CBA} = \widehat{DBA} (gt)\\ Cạnh BA chung \\ \widehat{BAC} = \widehat{BAD} (gt) \end{matrix}\right\}$

⇒ $\Delta BCA = \Delta BDA (g-c-g)$

– Hình 99: Ta có:

$\widehat{ABC}$ + $\widehat{ABD}$ = $180^0$ (hai góc kề bù)

⇒ $\widehat{ABD}$ = $180^0$ – $\widehat{ABC}$ (1)

$\widehat{ACB}$ + $\widehat{ACE}$ = $180^0$ (hai góc kề bù)

⇒ $\widehat{ACE}$ = $180^0$ – $\widehat{ACB}$ (2)

Mà $\widehat{ABC}$ = $\widehat{ACB}$ (3)

Từ (1), (2), (3) suy ra: $\widehat{ABD}$ = $\widehat{ACE}$.

Xét hai tam giác ABD và ACE có:

$\left.\begin{matrix} \widehat{ADB} = \widehat{AEC} (gt)\\ DB = CE (gt) \\ \widehat{ABD} = \widehat{ACE} (cmt) \end{matrix}\right\}$

⇒ $\Delta ABD = \Delta ACE (g-c-g)$

Ta có:

$DC = DB + BC$

$EB = EC + BC$

Mà $DB = EC ⇒ DC = EB$

Xét hai tam giác $ADC$ và $AEB$ có:

$\left.\begin{matrix} \widehat{ADC} = \widehat{AEB} (gt)\\ DC = EB (cmt) \\ \widehat{ACD} = \widehat{ABE} (gt) \end{matrix}\right\}$

⇒ $\Delta ADC = \Delta AEB (g-c-g)$

3. Giải bài 35 trang 123 sgk Toán 7 tập 1

Cho góc $xOy$ khác góc bẹt, $Ot$ là tia phân giác của góc đó. Qua điểm $H$ thuộc tia $Ot$, kẻ đường vuông góc với $Ot$, nó cắt $Ox$ và $Oy$ theo thứ tự ở $A$ và $B.$

a) Chứng minh rằng $OA = OB$.

b) Lấy điểm $C$ thuộc tia $Ot$, chứng minh rằng $CA = CB$ và $\widehat{OAC} = \widehat{OBC}$.

Bài giải:

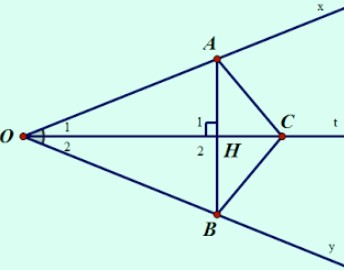
a) Xét hai tam giác vuông $HAO$ và $HBO$ có:

$\widehat{O_1}$ = $\widehat{O_2}$ (vì Ot là tia phân giác của $\widehat{xOy}$)

Cạnh $OH$ chung.

$\widehat{H_1}$ = $\widehat{H_2}$ = $90^0$

Vậy $\Delta HAO = \Delta HBO (g-c-g)$

Suy ra $OA = OB$ (hai cạnh tương ứng)

b) Xét hai tam giác $OAC$ và $OBC$ có:

$OA = OB (cmt)$

$\widehat{O_1}$ = $\widehat{O_2}$

Cạnh $OC$ chung.

Vậy $\Delta OAC = \Delta OBC (c-g-c)$

Suy ra $CA = CB$ và $\widehat{OAC}$ = $\widehat{OBC}$ (đpcm)

Bài trước:

Luyện tập 2: Giải bài 30 31 32 trang 120 sgk toán 7 tập 1

Bài tiếp theo:

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 7 với giải bài 33 34 35 trang 123 sgk toán 7 tập 1!

“Bài tập nào khó đã có giaibaisgk.com“