Nội Dung
Hướng dẫn giải Bài §6. Từ vuông góc đến song song, chương I – Đường thẳng vuông góc. Đường thẳng song song, sách giáo khoa toán 7 tập một. Nội dung bài giải bài 40 41 trang 97 sgk toán 7 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 7.
Lý thuyết
1. Quan hệ giữa tính vuông góc với tính song song
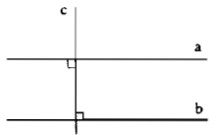
Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
2. Ba đường thẳng song song
Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.

Ba đường thẳng $d, d’, d’’$ song song với nhau từng đôi mội ta nói ba đường thẳng ấy song song với nhau.
Ký hiệu: $d // d’ // d’’.$
3. Ví dụ minh họa
Trước khi đi vào giải bài 40 41 trang 97 sgk toán 7 tập 1, chúng ta hãy tìm hiểu các ví dụ điển hình sau đây:
Ví dụ 1:
Trong hình, biết \(\widehat M = {120^0},\widehat N = {60^0}\) và \(\widehat F = {90^0}.\) Chứng minh \(a \bot c.\)
Bài giải:
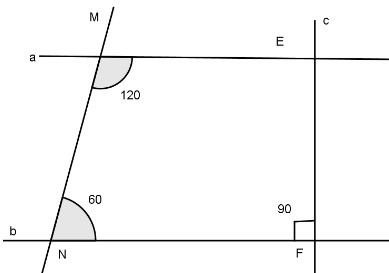
Ta có: \(\widehat M + \widehat N = {120^0} + {60^0} = {180^0},\) suy ra a//b (vì có cặp góc trong cùng phía bù nhau).
Ta có \(\widehat F = {90^0} \Rightarrow c \bot b,\) mà a // b nên \(c \bot a\)(hệ quả của định lý hai đường thẳng song song).
Ví dụ 2:
Trên hình bên ta có \(\widehat {ABC} = \widehat A + \widehat C.\) Hai đường thẳng Ax và Cy có song song với nhau hay không?
Bài giải:

Vẽ tia Bm sao cho \(\widehat {ABm}\) và \(\widehat A\) là hai góc so le trong và bằng nhau.
Ta có \(\widehat {ABm} = A \Rightarrow Ax//Bm\,\,\,{\,^{\,(1)}}\)
Tia Bm nằm giữa hai tia BA, BC nên \(\widehat {ABC} = \widehat {ABm} + \widehat {CBm}\)
Hay \(\widehat {ABC} = \widehat A + \widehat {CBm}\)
\(\widehat {ABC} = \widehat A + \widehat C\,\,\,\,(gt)\)Mặt khác
Suy ra \(\widehat C = \widehat {CBm}\)
Hai góc C và CBm bằng nhau ở vị trí so le trong nên Cy //Bm (2)
Từ (1) và (2) suy ra Ax // Cy.
\(xOy = {145^0}.\)
Ví dụ 3:
Cho góc Trên tia Ox lấy điểm A. Qua A vẽ tia Az sao cho tia Az và Oy nằm trên cùng một nửa mặt phẳng bờ chừa tia Ox và \(\widehat {OAz} = {35^0}.\)
a. Chứng minh: Az // Oy
b. Vẽ tia Az’ đối với tia Az. Chứng minh hai đường phân giác của hai góc xOy và OAz’ song song với nhau.
Bài giải:
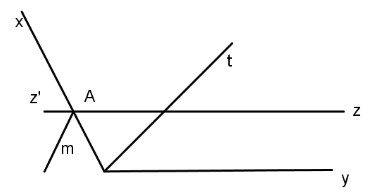
a. Ta có:
\(\begin{array}{l}\widehat {xOy} = {145^0}\,\,\,\,\,(gt)\\\widehat {OAz} = {35^0}\,\,\,\,\,\,\,\,(gt)\\ \Rightarrow \widehat {xOy} + \widehat {OAz} = {180^0}\end{array}\)
mà \(\widehat {xOy}\) và \(\widehat {OAz}\) ở vị trí góc trong cùng phía nên Az // Oy.
b. Gọi Ot phân giác \(\widehat {AOy}\) nên
\(\widehat {AOt} = \frac{1}{2}\widehat {AOy} = \frac{1}{2}{.145^0} = {72^0}30’\,\,{\,^{\,(1)}}\)
\(\widehat {OAz’}\)\(\widehat {OAz}\) kề bù mà \(\widehat {OAz} = {35^0}\) nên \(\widehat {OAz’} = {145^0}\)
Gọi Am là phân giác \(\widehat {OAz’}\) ta có: \(\widehat {OAm} = \frac{1}{2}\widehat {OAz’} = {72^0}30’\,\,{\,^{(2)}}\)
Từ (1) và (2) suy ra \(\widehat {OAm} = \widehat {AOt.}\)
\(\widehat {OAm}\)
Mà và \(\widehat {AOt}\) ở vị trí so le trong
Nên Am // Ot.
Ví dụ 4:
Phát biểu nào sau đây là sai?
A. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
B. Cho hai đường thẳng song song a và b. Nếu đường thẳng d vuông góc với a thì d cũng vuông góc với b.
C. Với ba đường thẳng a, b và c. Nếu \(a \bot b\) và \(b \bot c\) thì \(a \bot c.\)
D. Hai đường thẳng x’x và y’y cắt nhau tại O nếu \(\widehat {xOy} = {90^0}\) thì ba góc còn lại cũng là góc vuông.
Bài giải:
\(a \bot b,b \bot c\)Nếu thì a//c do đó C là sai. Vậy chọn C.
Ví dụ 5:
Cho góc nhọn xOy. \(QR \bot Ox.\)Từ điểm M trên cạnh Ox, dựng \(MN \bot Oy;\) dựng \(NP \bot Ox;\) dựng
a. Chứng minh MN // PQ; NP // QR.
b. Tìm góc bằng góc PMN.
c. Chứng minh \(\widehat {MNP} = \widehat {NPQ} = \widehat {PQR};\widehat {PNQ} = \widehat {RQO};\,\,\widehat {QPR} = \widehat {NMP}.\)
Bài giải:
a. Ta có
\(\begin{array}{l}MN \bot Oy\,\,\,(gt)\\PQ \bot Oy\,\,\,\,(gt)\end{array}\)
Nên MN // PQ.
NP//QR (cùng vuông góc với Ox)
b. Ta có:
\(\widehat {PMN} = \widehat {RPQ}\) (đồng vị)
c. Ta có:
\(\widehat {MNP} = \widehat {NPQ}\) (so le trong của MN // PQ)
\(\widehat {MNP} = \widehat {PQR}\) (so le trong của NP // QR)
Vậy \(\widehat {MNP} = \widehat {NPQ} = \widehat {PQR}.\)
\(\widehat {PNQ} = \widehat {RQO}\) (đồng vị của NP//QR)
\(\widehat {QPR} = \widehat {NMP}\) (đồng vị)
Vậy \(\widehat {PNQ} = \widehat {RQO};\,\,\widehat {QPR} = \widehat {NMP}.\)
Ví dụ 6:
Cho \(\widehat {xOy} = \alpha ,\) điểm A nằm trên Oy. Qua A vẽ tia Am. Tính số đo góc \(\widehat {OAm}\) để \(Am//Ox.\)
Bài giải:
Xét vị trí của tia Am với góc xOy, có 2 trường hợp:
Tia Am thuộc miền trong góc xOy
Tia Am thuộc miền ngoài góc xOy.
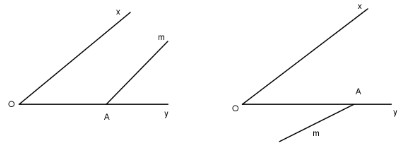
Ta có:
– Tia Am thuộc miền trong góc xOy thì có \(\widehat {OAm}\) và \(\widehat {xOy}\) là 2 góc trong cùng phía.
Để Am // Ox thì phải có \(\widehat {xOy} + \widehat {OAm} = {180^0}\,\,hay\,\,\,\alpha + \widehat {OAm} = {180^0}.\)
Suy ra \(\widehat {OAm} = {180^0} – \alpha \)
– Tia Am thuộc miền ngoài góc xOy thì \(\widehat {xOy}\) và \(\widehat {OAm}\) là 2 góc so le trong.
Vậy để Am // Ox thì \(\widehat {OAm} = \widehat {xOy} = \alpha \).
Dưới đây là phần Hướng dẫn trả lời các câu hỏi có trong bài học cho các bạn tham khảo. Các bạn hãy đọc kỹ câu hỏi trước khi trả lời nhé!
Câu hỏi
1. Trả lời câu hỏi 1 trang 96 sgk Toán 7 tập 1
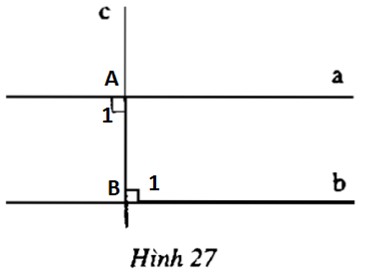
Xem hình \(27\), (cho biết \(a⏊c\) và \(b⏊c\))
a) Dự đoán xem \(a\) và \(b\) có song song với nhau không?
b) Sử dụng dấu hiệu nhận biết hai đường thẳng song song (Bài 4) hãy suy ra \(a//b\).
Trả lời:
a) Dự đoán: \(a\) và \(b\) có song song với nhau.
b) Góc \({A_1}\) và góc \({B_1}\) là hai góc so le trong và \(\widehat {{A_1}} = \widehat {{B_1}} = {90^o}\) nên theo dấu hiệu nhận biết hai đường thẳng song song thì \(a//b\).
2. Trả lời câu hỏi 2 trang 97 sgk Toán 7 tập 1
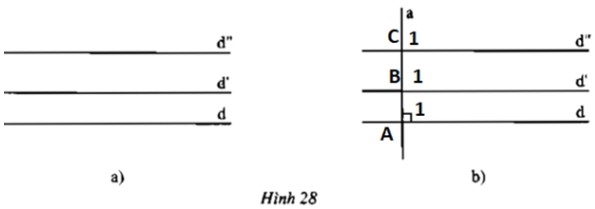
Xem hình 28a (cho biết \(d’//d\) và \(d’’//d\))
a) Dự đoán xem \(d’\) và \(d’’\) có song song với nhau không?
b) Vẽ đường thẳng \(a\) vuông góc với \(d\) (như hình 28b) rồi trả lời các câu hỏi sau:
• \(a\) có vuông góc với \(d’\) không? Vì sao?
• \(a\) có vuông góc với \(d’’\) không? Vì sao?
• \(d’\) có song song với \(d’’\) không? Vì sao?
Trả lời:
Ta có:
a) Dự đoán: \(d’\) và \(d’’\) có song song với nhau.
b) Vì \(a\) vuông góc với \(d \Rightarrow \widehat {{A_1}} = {90^o}\)
• \(a\) có vuông góc với \(d’\).
Vì \(d//d’\)
\( \Rightarrow \widehat {{A_1}} = \widehat {{B_1}}\) ( hai góc đồng vị)
\( \Rightarrow \widehat {{B_1}} = {90^o}\)
• \(a\) có vuông góc với \(d’’\)
Vì \(d//d’’\) \( \Rightarrow \widehat {{A_1}} = \widehat {{C_1}}\) (hai góc đồng vị)
\( \Rightarrow \widehat {{C_1}} = {90^o}\)
• \(d’\) có song song với \(d’’\)
Vì \(\widehat {{B_1}} = \widehat {{C_1}} = {90^o}\) mà hai góc ở vị trí đồng vị.
Dưới đây là Hướng dẫn giải bài 40 41 trang 97 sgk toán 7 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 7 kèm bài giải chi tiết bài 40 41 trang 97 sgk toán 7 tập 1 của bài §6. Từ vuông góc đến song song trong chương I – Đường thẳng vuông góc. Đường thẳng song song cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
1. Giải bài 40 trang 97 sgk Toán 7 tập 1
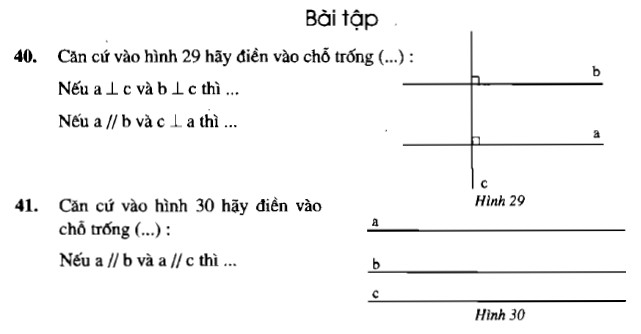
Căn cứ vào hình 29, hãy điền vào chỗ trống (…):
Nếu $a \perp c$ và $b \perp c$ thì…
Nếu $a // b$ và $c \perp a$ thì …

Bài giải:
Theo tính chất về quan hệ giữa tính vuông góc và tính song song, ta điền như sau:
– Nếu $a \perp c$ và $b \perp c$ thì $a // b$
– Nếu $a // b$ và $c \perp a$ thì $b \perp c$
2. Giải bài 41 trang 97 sgk Toán 7 tập 1
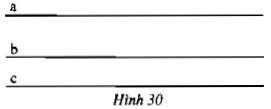
Căn cứ vào hình 30 hãy điền vào chỗ trống (…):
Nếu $a // b$ và $a // c$ thì …
Bài giải:
Theo tính chất về ba đường thẳng song song, chỗ trống được điền như sau:
Nếu $a // b$ và $a // c$ thì $b // c$.
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 7 khác
- Để học tốt môn Vật lí lớp 7
- Để học tốt môn Sinh học lớp 7
- Để học tốt môn Ngữ văn lớp 7
- Để học tốt môn Lịch sử lớp 7
- Để học tốt môn Địa lí lớp 7
- Để học tốt môn Tiếng Anh lớp 7
- Để học tốt môn Tiếng Anh lớp 7 thí điểm
- Để học tốt môn Tin học lớp 7
- Để học tốt môn GDCD lớp 7
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 7 với giải bài 40 41 trang 97 sgk toán 7 tập 1!
“Bài tập nào khó đã có giaibaisgk.com“
