Nội Dung
Luyện tập Bài §9. Thể tích của hình chóp đều, Chương IV – Hình lăng trụ đứng – Hình chóp đều, sách giáo khoa toán 8 tập hai. Nội dung bài giải bài 47 48 49 50 trang 124 125 sgk toán 8 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 8.
Lý thuyết
Công thức tính thể tích
Thể tích của hình chóp đều bằng một phần ba diện tích mặt đáy nhân với chiều cao
$V = \frac{1}{3}.S.h$
Trong đó:
S: diện tích đáy
h: chiều cao
Dưới đây là Hướng dẫn giải bài 47 48 49 50 trang 124 125 sgk toán 8 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Luyện tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 8 kèm bài giải chi tiết bài 47 48 49 50 trang 124 125 sgk toán 8 tập 2 của Bài §9. Thể tích của hình chóp đều trong Chương IV – Hình lăng trụ đứng – Hình chóp đều cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
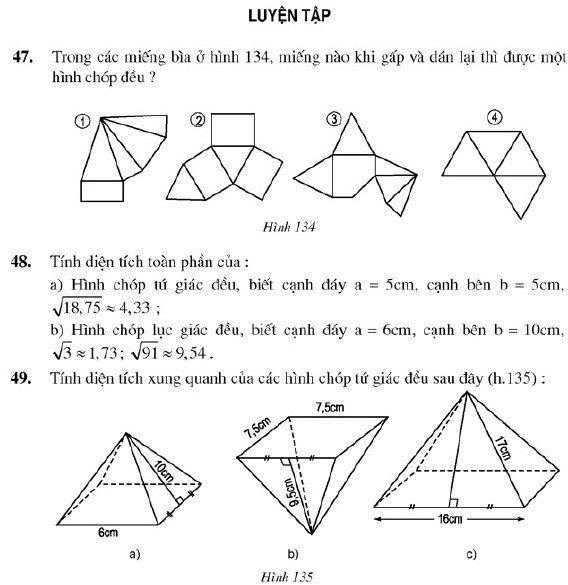
1. Giải bài 47 trang 124 sgk Toán 8 tập 2
Trong các miếng bìa ở hình 134, miếng nào khi gấp và dán lại thì được một hình chóp đều?

Bài giải:
– Hình 1: Khi gấp lại không được hình chóp đều vì hình chóp thu được có đáy là hình chữ nhật. Không là đa giác đều.
– Hình 2: Khi gấp lại ta được hình lăng trụ đứng đáy tam giác đều, không phải là hình chóp tam giác đều.
– Hình 3: Khi gấp lại không được hình chóp tam giác đều vì hình chóp thu được có được đáy là hình ngũ giác không phải là ngũ giác đều.
– Hình 4: Khi gấp lại không được hình chóp đều vì hình thu được là hình chóp đều thiếu một mặt đáy và dư một mặt bên.

2. Giải bài 48 trang 125 sgk Toán 8 tập 2
Tính diện tích toàn phần của:
a) Hình chóp tứ giác đều, biết cạnh đáy \(a = 5cm\), cạnh bên \(b = 5cm,\;\sqrt{18,75}\approx 4,33 \).
b) Hình chóp lục giác đều, biết cạnh đáy \(a = 6cm\), cạnh bên \(b = 10cm,\; \sqrt{3}\approx 1,73; \;\sqrt{91}\approx 9,54\).
Bài giải:
a) Chóp đều tứ giác S.ABCD có đáy là hình vuông ABCD cạnh \(5cm\); mặt bên là các tam giác đều cạnh \(5cm\).

Ta có các mặt bên của hình chóp đều là những tam giác đều cạnh \(5cm\).
Đường cao của mỗi mặt bên là:
\(SH = \sqrt{SA^{2} -HA^{2}}\)
\(= \sqrt{5^{2} -2,5^{2}}= \sqrt{18,75}\approx 4,33 (cm) \)
Diện tích xung quanh hình chóp là:
\(S_{xq} = p.d = \dfrac{1}{2}. 5.4.4,33 = 43,3 (cm^2) \)
Diện tích đáy hình chóp:
\(S_{đ} = a^2 = 5^2 =25(cm^2) \)
Diện tích toàn phần hình chóp:
\( S_{tp} = S_{xq}+ S_{đ} = 43,3 + 25 = 68,3 \) \((cm^2)\)
b) Hình chóp lục giác đều S.MNRQPO. Mặt bên của hình chóp lục giác đều là tam giác cân có cạnh bên \(10cm\), cạnh đáy \(6cm\).

Gọi K là trung điểm MN ⇒ Đường cao SK của mặt bên là:
\(SK = \sqrt{SM^{2} -MK^{2}} = \sqrt{10^{2} -3^{2}} \) \(= \sqrt{91}\approx 9,54 (cm) \)
Diện tích xung quanh hình chóp:
\(S_{xq} = p.d = \dfrac{1}{2}. 6.6.9,54 = 171,72\) \( (cm^2) \)
Đáy của hình chóp là lục giác đều. Diện tích lục giác bằng \(6\) lần diện tích tam giác đều \(MNH\).
Chiều cao của tam giác đều là:
\(HK = \sqrt{HM^{2} -MK^{2}} = \sqrt{6^{2} -3^{2}}\) \(= \sqrt{27}\approx 5,2 (cm) \)
Diện tích đáy hình chóp:
\(S_{đ} =6. \dfrac{1}{2}6.5,2 = 93,6(cm^2) \)
Diện tích toàn phần hình chóp:
\( S_{tp} = S_{xq}+ S_{đ} = 171,72 + 93,6 \) \(= 265,32 (cm^2)\)
3. Giải bài 49 trang 125 sgk Toán 8 tập 2
Tính diện tích xung quanh của các hình chóp tứ giác đều sau đây (h.135)

Bài giải:
a) Hình a):
Diện tích xung quanh của hình chóp là:
\(S_{xq} = p.d = \dfrac{1}{2}. 6.4.10 = 120 (cm^2)\)
b) Hình b):
Diện tích xung quanh của hình chóp là:
\(S_{xq} = p.d = \dfrac{1}{2}. 7,5.4.9,5 = 142,5\) \( (cm^2)\)
c) Hình c):
Độ dài trung đoạn của hình chóp là :
\(d = \sqrt{17^{2} -8^{2}} = \sqrt{289 -64}= \sqrt{225} \) \(= 15(cm) \)
Diện tích xung quanh của hình chóp là:
\(S_{xq} = p.d = \dfrac{1}{2}. 16.4.15 = 480 (cm^2)\)
4. Giải bài 50 trang 125 sgk Toán 8 tập 2
a) Tính thể tích của hình chóp đều (h.136).
b) Tính diện tích xung quanh của hình chóp cụt đều (h.137).
(Hướng dẫn: Diện tích cần tính bằng tổng diện tích các mặt xung quanh. Các mặt xung quanh là những hình thang cân với cùng chiều cao, các cạnh đáy tương ứng bằng nhau, các cạnh bên bằng nhau).

Bài giải:
a) Diện tích đáy của hình chóp đều:
\( S = BC^2 = 6,5^2 = 42,25 (cm^2)\)
Thể tích hình chóp đều là:
\( V = \dfrac{1}{3} .S.h = \dfrac{1}{3} . 42,25 .12 = 169\)\(\, (cm^3)\)
b) Các mặt xung quanh là những hình thang cân đáy nhỏ \(2cm\), đáy lớn \(4cm\) , chiều cao \(3,5cm\).
Diện tích xung quanh của hình chóp cụt đều là:
\(S_{xq} = 4. \dfrac{(2+4). 3,5}{2} =42 (cm^2) \)
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 8 khác
- Để học tốt môn Vật lí lớp 8
- Để học tốt môn Sinh học lớp 8
- Để học tốt môn Ngữ văn lớp 8
- Để học tốt môn Lịch sử lớp 8
- Để học tốt môn Địa lí lớp 8
- Để học tốt môn Tiếng Anh lớp 8
- Để học tốt môn Tiếng Anh lớp 8 thí điểm
- Để học tốt môn Tin học lớp 8
- Để học tốt môn GDCD lớp 8
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 8 với giải bài 47 48 49 50 trang 124 125 sgk toán 8 tập 2!
“Bài tập nào khó đã có giaibaisgk.com“
