Nội Dung
Luyện tập Bài §12. Hình vuông, chương I – Tứ giác, sách giáo khoa toán 8 tập một. Nội dung bài giải bài 83 84 85 86 trang 109 sgk toán 8 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 8.
Lý thuyết
1. Định nghĩa
Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.

Từ định nghĩa này ta suy ra:
– Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.
– Hình vuông là hình thoi có bốn góc vuông.
2. Tính chất
Vì hình vuông vừa là hình chữ nhật, vừa là hình thoi nên hình vuông có tất cả tính chất của hình chữ nhật (Chẳng hạn: hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường) và có tất cả các tính chất của hình thoi (chẳng hạn: hai đường chéo vuông góc với nhau và mỗi đường chéo là phân giác của các góc ở đỉnh), đặc biệt ta có thể phát biểu định lí:
Trong hình vuông, hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
3. Dấu hiệu nhận biết
- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
- Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
- Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.
- Hình thoi có một góc vuông là hình vuông.
- Hình thoi có hai đường chéo bằng nhau là hình vuông.
Dưới đây là Hướng dẫn giải bài 83 84 85 86 trang 109 sgk toán 8 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Luyện tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 8 kèm bài giải chi tiết bài 83 84 85 86 trang 109 sgk toán 8 tập 1 của bài §12. Hình vuông trong chương I – Tứ giác cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 83 trang 109 sgk Toán 8 tập 1
Các câu sau đúng hay sai?
a) Tứ giác có hai đường chéo vuông góc với nhau là hình thoi.
b) Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi.
c) Hình thoi là tứ giác có tất cả các cạnh bằng nhau.
d) Hình chữ nhật có hai đường chéo bằng nhau là hình vuông.
e) Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
Bài giải:
Dựa vào dấu hiệu nhận biết, ta nhận thấy:
a) Sai. Hình bình hành có hai đường chéo vuông góc mới là hình thoi, còn tứ giác thì chưa đủ.
b) Hai đường chéo cắt nhau tại trung điểm của mỗi đường thì tứ giác đó là hình bình hành rồi. Mà hình bình hành đó lại có hai đường chéo vuông góc nhau, chẳng phải đó là hình thoi sao. Vậy khẳng định b) là đúng.
c) Khẳng định này chắc chắn là đúng rồi, hình thoi được định nghĩa như vậy mà.
d) Câu này sai, không có cơ sở nào để khẳng định điều đó.
e) Khẳng định này đúng, đó chính là dấu hiệu thứ hai để nhận biết hình vuông.
2. Giải bài 84 trang 109 sgk Toán 8 tập 1
Cho tam giác $ABC, D$ là điểm nằm giữa $B$ và $C$. Qua $D$ kẻ các đường thẳng song song với $AB$ và $AC$, chúng cắt các cạnh $AC$ và $AB$ theo thứ tự ở $E$ và $F$.
a) Tứ giác $AEDF$ là hình gì? Vì sao?
b) Điểm $D$ ở vị trí nào trên cạnh $BC$ thì tứ giác $AEDF$ là hình thoi.
c) Nếu tam giác $ABC$ vuông tại $A$ thì tứ giác $AEDF$ là hình gì. Điểm $D$ ở vị trí nào trên cạnh $BC$ thì tứ giác $AEDF$ là hình vuông?
Bài giải:
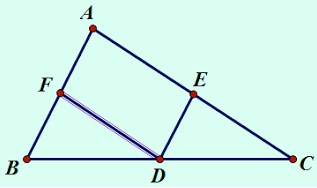
a) Ta có:
$\left.\begin{matrix} DE // AB (gt)\\ DF // AC (gt) \end{matrix}\right\}$
⇒ Tứ giác $AEDF$ là hình bình hành.
b) Theo dấu hiệu nhận biết thì hình bình hành $AEDF$ là hình thoi khi đường chéo $AD$ là phân giác $\widehat{BAC}$.
Khi đó $D$ sẽ là giao điểm của phân giác $\widehat{BAC}$ với cạnh $BC$ của tam giác $ABC.$
c) Ta có: $AEDF$ là hình bình hành (cmt)
$\widehat{A} = 90^0$ (tam giác $ABC$ vuông tại $A$)
Suy ra $AEDF$ là hình chữ nhật.
Hình chữ nhật có một đường chéo là phân giác của một góc là hình vuông. Nên để hình chữ nhật $AEDF$ là hình vuông thì $D$ phải là giao điểm của đường phân giác góc $A$ với cạnh huyền $BC$ của tam giác $ABC.$
3. Giải bài 85 trang 109 sgk Toán 8 tập 1
Cho hình chữ nhật $ABCD$ có $AB = 2AD$. Gọi $E, F$ theo thứ tự là trung điểm của $AB, CD$. Gọi $M$ là giao điểm của $AF$ và $DE, N$ là giao điểm của $BF$ và $CE.$
a) Tứ giác $ADFE$ là hình gì? Vì sao?
b) Tứ giác $EMFN$ là hình gì? Vì sao?
Bài giải:

a) Tứ giác \(ADFE\) là hình vuông.
Giải thích:
Tứ giác \(ADFE\) có \(AE // DF\), \(AE = DF\) nên là hình bình hành.
Hình bình hành \(ADFE\) có \(\widehat{A} = 90^0\) nên là hình chữ nhật.
Theo giả thiết \(AB=2AD\) mà \(AE={AB\over 2}\) nên \(AE=AD={AB\over 2}\)
Hình chữ nhật \(ADFE\) có \(AE = AD\) nên là hình vuông.
b) Tứ giác \(EMFN\) là hình vuông.
Giải thích:
Tứ giác \(DEBF\) có \(EB // DF, EB = DF\) nên là hình bình hành.
Do đó \(DE // BF\)
Tương tự \(AF // EC\)
Suy ra \(EMFN\) là hình bình hành.
Theo câu a, \(ADFE\) là hình vuông nên \(ME = MF, ME ⊥ MF\).
Hình bình hành \(EMFN\) có \(\widehat{M} = 90^0\) nên là hình chữ nhật, lại có \(ME = MF\) nên là hình vuông.
4. Giải bài 86 trang 109 sgk Toán 8 tập 1
Đố. Lấy một tờ giấy gấp làm tư rồi cắt chéo theo nhát cắt $AB$ (h.108). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác nhận được là hình gì? Vì sao? Nếu ta có $OA = OB$ thì tứ giác nhận được là hình gì?

Bài giải:
Tứ giác nhận được theo nhát cắt $AB$ là hình thoi vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau. Nếu có thêm $OA = OB$ thì hình thoi nhận được có hai đường chéo bằng nhau nên là hình vuông.
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 8 khác
- Để học tốt môn Vật lí lớp 8
- Để học tốt môn Sinh học lớp 8
- Để học tốt môn Ngữ văn lớp 8
- Để học tốt môn Lịch sử lớp 8
- Để học tốt môn Địa lí lớp 8
- Để học tốt môn Tiếng Anh lớp 8
- Để học tốt môn Tiếng Anh lớp 8 thí điểm
- Để học tốt môn Tin học lớp 8
- Để học tốt môn GDCD lớp 8
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 8 với giải bài 83 84 85 86 trang 109 sgk toán 8 tập 1!
“Bài tập nào khó đã có giaibaisgk.com“
