Hướng dẫn Giải bài 1 2 3 4 5 6 trang 40 sgk Hình học 10

Nội Dung

Hướng dẫn giải Bài §1. Giá trị lượng giác của một góc bất kỳ từ 0 độ đến 180 độ, Chương II. Tích vô hướng của hai vectơ và ứng dụng, sách giáo khoa Hình học 10. Nội dung bài giải bài 1 2 3 4 5 6 trang 40 sgk Hình học 10 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập hình học có trong SGK để giúp các em học sinh học tốt môn toán lớp 10.

Lý thuyết

Trước khi đi vào định nghĩa, ta xét hình sau:

Hình trên mô phỏng một nửa đường tròn có bán kín bằng 1. Ta gọi nó là nửa đường tròn đơn vị.

Điểm M thuộc nửa đường tròn ấy, vậy góc cho trước có độ lớn từ 0 độ đến 180 độ.

1. Định nghĩa

Với mỗi góc $α$ $({0^0} \le \alpha \le {180^0})$ ta xác định một điểm $M$ trên nửa đường tròn đơn vị sao cho góc $\widehat{xOM} = α$ và giả sử điểm $M$ có tọa độ $M({x_0};{y_0})$.

Khi đó ta có định nghĩa:

$Sin$ của góc $α$ là ${y_0}$, kí hiệu là $\sin α = {y_0}$

$cosin$ của góc $α$ là $x_0$, kí hiệu là $\cos α =x_0$

$tang$ của góc $α$ là $( x_0≠ 0)$, ký hiệu $\tan α =\frac{x_{0}}{y_{0}}$

$cotang$ cuả góc $α$ là $(y_0≠ 0)$, ký hiệu $\cot α = \frac{y_{0}}{x_{0}}$

Các số $\sin α$, $\cos α$, $\tan α$, $\cot α$ được gọi là các giá trị lượng giác của góc $ α$

2. Tính chất

Sự liên hệ giữa các giá trị lượng giác của các góc bù nhau:

$\sin α = \sin(180^0– α)$

$\cos α = -\cos((180^0– α)$

$\tan α = -\tan(180^0– α)$

$\cot α = – \cot(180^0– α)$

Hai góc bù nhau thì có sin bằng nhau còn cos, tan, cot thì đối nhau

3. Bảng giá trị lượng giác của các góc đặc biệt

Góc	$0^0$	$30^0$	$45^0$	$60^0$	$90^0$	$180^0$
sin	$0$	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	$1$	$0$
cos	$1$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	$0$	$-1$
tan	$0$	$\frac{1}{\sqrt{3}}$	$1$	$\sqrt{3}$	$\parallel$	$0$
cot	$\parallel$	$\sqrt{3}$	$1$	$\frac{1}{\sqrt{3}}$	$0$	$\parallel$

4. Góc giữa hai vectơ

Định nghĩa: Cho hai vectơ $\vec{a}$ và $\vec{b}$ đều khác vectơ $0$. Từ một điểm $0$ bât kỳ ta vẽ $\vec{a}$

và $\vec{b}$ đều khác vec tơ $0$. Từ một điểm $O$ bất kỳ ta vẽ $\vec{OA}$ = $\vec{a}$ và $\vec{OB}$ = $\vec{b}$ góc $\widehat{AOB}$ với số đo từ $0^0$ đến $180^0$ độ được gọi là góc giữa hai vectơ $\vec{a}$ và $\vec{b}$.

Người ta ký hiệu góc giữa hai vectơ $\vec{a}$ và $\vec{b}$ là ($\vec{a}$;$\vec{b}$) Nếu $(\vec{a};\vec{b})= 90^0$ thì ta nói rằng $\vec{a}$ và $\vec{b}$ vuông góc với nhau. Ký hiệu là $\vec{a}$ ⊥ $\vec{b}$ hoặc $\vec{b}$ ⊥ $\vec{a}$

Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong mục hoạt động của học sinh trên lớp sgk Hình học 10.

Câu hỏi

1. Trả lời câu hỏi 1 trang 35 sgk Hình học 10

Tam giác $ABC$ vuông tại $A$ có góc nhọn $\widehat{ABC}$ $= α$. Hãy nhắc lại định nghĩa các tỉ số lượng giác của góc nhọn $α$ đã học ở lớp 9.

Trả lời:

Định nghĩa các tỉ số lượng giác của góc nhọn α đã học ở lớp 9:

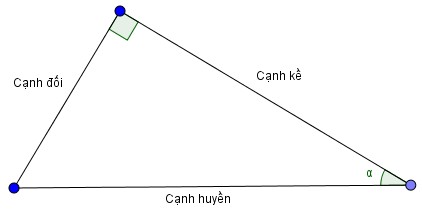
Với tam giác $ABC$ vuông tại $A$ có góc nhọn $\widehat{ABC}$ $= α$ ta có:

$sin α = \frac{AC}{BC}$; $cos α = \frac{AB}{BC}$;

$tan α = \frac{AC}{AB}$; $cot α = \frac{AB}{AC}$.

2. Trả lời câu hỏi 2 trang 35 sgk Hình học 10

Trong mặt phẳng tọa độ $Oxy$, nửa đường tròn tâm $O$ nằm phía trên trục hoành bán kính $R = 1$ được gọi là nửa đường tròn đơn vị (h.2.2). Nếu cho trước một góc nhọn $α$ thì ta có thể xác định một điểm $M$ duy nhất trên nửa đường tròn đơn vị sao cho $\widehat{xOM}$ $= α$. Giả sử điểm $M$ có tọa độ (x_o; y_o).

Hãy chứng tỏ rằng sinα = y_o, cosα = x_o, tanα =$\frac{y_0}{x_0}$, cotα = $\frac{x_0}{y_0}$.

Trả lời:

Áp dụng công thức tính tỉ số lượng giác góc α trong tam giác vuông 0MX_o ta có:

$sin α = \frac{Mx_0}{OM}$ = y_o;

$cos α = \frac{0x_0}{OM}$ = x_o;

$tan α = \frac{Mx_0}{0x_0}$ = $\frac{y_0}{x_0}$ ;

$cot α = \frac{0x_0}{0x_0}$ = $\frac{x_0}{y_0}$.

3. Trả lời câu hỏi 3 trang 38 sgk Hình học 10

Tìm các giá trị lượng giác của các góc 120^o, 150^o.

Trả lời:

♦ Các giá trị lượng giác của góc 120^o là:

sin ⁡120^o = sin⁡ (180^o – 120^o ) = sin⁡ 60^o = $\frac{\sqrt{3}}{2}$

cos⁡ ⁡120^o = -cos⁡ (180^o – 120^o )= -cos⁡ 60^o = -$\frac{1}{2}$

tan ⁡120^o = -tan (180^o – 120^o ) = -tan⁡ 60^o = -$\sqrt{3}$

cot ⁡120^o = -cot⁡ (180^o – 120^o )= -cot⁡ 60^o = -$\frac{1}{\sqrt{3}}$

♦ Các giá trị lượng giác của góc 150^o là:

sin⁡ 150^o= sin⁡ (180^o – 150^o ) = sin ⁡30^o = $\frac{1}{2}$

cos⁡ 150^o= -cos⁡ (180^o – 150^o ) = -cos ⁡30^o = -$\frac{\sqrt{3}}{2}$

tan⁡ 150^o= -tan (180^o – 150^o ) = -tan ⁡30^o = -$\frac{1}{\sqrt{3}}$

cot⁡ 150^o= -cot⁡ (180^o – 150^o ) = -cot⁡ 30^o = -$\sqrt{3}$

4. Trả lời câu hỏi 4 trang 38 sgk Hình học 10

Khi nào góc giữa hai vectơ bằng 0^o ? Khi nào góc giữa hai vectơ bằng 180^o.

Trả lời:

Góc giữa hai vectơ bằng 0^o khi chúng cùng hướng với nhau.

Góc giữa hai vectơ bằng 180^o khi chúng ngược hướng với nhau.

Dưới đây là phần Hướng dẫn giải bài 1 2 3 4 5 6 trang 40 sgk Hình học 10. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập hình học 10 kèm bài giải chi tiết bài 1 2 3 4 5 6 trang 40 sgk Hình học 10 của Bài §1. Giá trị lượng giác của một góc bất kỳ từ 0 độ đến 180 độ trong Chương II. Tích vô hướng của hai vectơ và ứng dụng cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 6 trang 40 sgk Hình học 10

1. Giải bài 1 trang 40 sgk Hình học 10

Chứng minh rằng trong tam giác $ABC$ có:

a) $\sin A = \sin(B + C)$

b) $\cos A = -\cos(B + C)$

Bài giải:

a) Xét $ΔABC$ có: $\widehat{A}+(\widehat{B}+\widehat{C})= 180^{\circ}$

⇔ $\widehat{A}=180^{\circ}-(\widehat{B}+\widehat{C})$

⇒ $\widehat{A}$ và $(\widehat{B}+\widehat{C})$ bù nhau.

Theo tính chất của hai góc bù nhau thì: $\sin A = \sin(B + C)$ (đpcm)

b) Tương tự câu a), ta có: $\cos A = -\cos (B+C)$ (đpcm)

2. Giải bài 2 trang 40 sgk Hình học 10

Cho $AOB$ là tam giác cân tại $O$ có $OA = a$ và có các đường cao $OH$ và $AK$. Giả sử$\widehat{AOH}=\alpha $.

Tính $AK$ và $OK$ theo $a$ và $\alpha$.

Bài giải:

Ta có: $OH$ là đường cao của tam giác cân $AOB$

⇒ $OH$ là tia phân giác của $\widehat{AOB}$

⇒ $\widehat{AOB}=2\alpha $.

Xét $\triangle AOK$ vuông tại $K$, ta có:

$\frac{AK}{AO}=\sin 2\alpha ⇒ AK=a\sin 2\alpha $

Tương tự: $\frac{OK}{AO}=\cos 2\alpha ⇒ OK=a\cos 2\alpha $

3. Giải bài 3 trang 40 sgk Hình học 10

Chứng minh rằng:

a) $\sin 105^{\circ} = \sin 75^{\circ}$

b) $\cos 170^{\circ} = -\cos 10^{\circ}$

c) $\cos 122^{\circ} = -\cos 58^{\circ}$

Bài giải:

Áp dụng tính chất lượng giác của hai góc bù nhau. ta có:

a) Ta có: $ 105^{\circ}= 180^{\circ}-75^{\circ}$

⇒ $\sin 105^{\circ}=\sin 75^{\circ}$

b) Ta có: $ 170^{\circ}= 180^{\circ}-10^{\circ}$

⇒ $\cos 170^{\circ}=-\cos 10^{\circ}$

c) Ta có: $ 122^{\circ}= 180^{\circ}-58^{\circ}$

⇒ $\cos 122^{\circ}=-\cos 58^{\circ}$

4. Giải bài 4 trang 40 sgk Hình học 10

Chứng minh rằng với mọi góc $\alpha $ $(0^{\circ}\leq \alpha \leq 180^{\circ})$ ta đều có $\cos ^{2}\alpha +\sin ^{2}\alpha =1$.

Bài giải:

Vẽ đường tròn lượng giác $C(O; 1)$. Theo định nghĩa, điểm $M(x_{0}; y_{0})$ thuộc đường tròn có:

$\sin \alpha =y_{0}$

$\cos \alpha =x_{0}$

Áp dụng định lí Pitago ta có:

$x_{0}^{2}+y_{0}^{2}=OM^{2}=1$

⇒$\cos ^{2}\alpha +\sin ^{2}\alpha =1$. (đpcm)

5. Giải bài 5 trang 40 sgk Hình học 10

Cho góc x, với $\cos x=\frac{1}{3}$. Tính giá trị của biểu thức: $P = 3\sin ^{2}\alpha+\cos ^{2}\alpha$

Bài giải:

Ta có: $\cos ^{2}\alpha +\sin ^{2}\alpha =1$.

⇒ $\sin ^{2}\alpha =1-\cos ^{2}\alpha$.

⇒ $\sin ^{2}\alpha =1-(\frac{1}{3})^{2}=\frac{8}{9}$.

Mặt khác: $P = 3\sin ^{2}\alpha+\cos ^{2}\alpha = 2\sin ^{2}\alpha+\sin ^{2}\alpha+\cos ^{2}\alpha=2\sin ^{2}\alpha+1$

⇔ $P=2.\frac{8}{9}+1=\frac{25}{9}$

Vậy $P=\frac{25}{9}$

6. Giải bài 6 trang 40 sgk Hình học 10

Cho hình vuông $ABCD$. Tính:

$\cos (\overrightarrow{AC},\overrightarrow{BA})$

$\sin (\overrightarrow{AC},\overrightarrow{BD})$

$\cos (\overrightarrow{AB},\overrightarrow{CD})$

Bài giải:

Ta có: $ (\overrightarrow{AC},\overrightarrow{BA})=135^{\circ}$

⇒ $\cos (\overrightarrow{AC},\overrightarrow{BA})=\frac{-\sqrt{2}}{2}$

Tương tự:

$ (\overrightarrow{AC},\overrightarrow{BD})=90^{\circ}$

⇒ $\sin (\overrightarrow{AC},\overrightarrow{BD})=1$

$ (\overrightarrow{AB},\overrightarrow{CD})=180^{\circ}$

⇒ $\cos (\overrightarrow{AB},\overrightarrow{CD})=-1$

Bài trước:

Trả lời câu hỏi trắc nghiệm 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 trang 28 29 30 31 32 sgk Hình học 10

Bài tiếp theo:

Giải bài 1 2 3 4 5 6 7 trang 45 46 sgk Hình học 10

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 10 với giải bài 1 2 3 4 5 6 trang 40 sgk Hình học 10!

“Bài tập nào khó đã có giaibaisgk.com“

Góc	\(0^0\)	\(30^0\)	\(45^0\)	\(60^0\)	\(90^0\)	\(180^0\)
sin	$0$	\(\frac{1}{2}\)	\(\frac{\sqrt{2}}{2}\)	\(\frac{\sqrt{3}}{2}\)	$1$	$0$
cos	$1$	\(\frac{\sqrt{3}}{2}\)	\(\frac{\sqrt{2}}{2}\)	\(\frac{1}{2}\)	$0$	$-1$
tan	$0$	\(\frac{1}{\sqrt{3}}\)	$1$	\(\sqrt{3}\)	\(\parallel\)	$0$
cot	\(\parallel\)	\(\sqrt{3}\)	$1$	\(\frac{1}{\sqrt{3}}\)	$0$	\(\parallel\)