Toán lớp 12

Giải bài 1 2 3 4 5 6 trang 68 sgk Hình học 12

Hướng dẫn giải Bài §1. Hệ tọa độ trong không gian, Chương III. Phương pháp toạ độ trong không gian, sách giáo khoa Hình học 12. Nội dung bài giải bài 1 2 3 4 5 6 trang 68 sgk Hình học 12 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập hình học có trong SGK để giúp các em học sinh học tốt môn toán lớp 12.

Lý thuyết

1. Tọa độ của điểm và của vectơ

a) Hệ tọa độ

Trong không gian, cho ba trục $4xOx’, yOy’, zOz’$ vuông góc với nhau từng đôi một.

Các vectơ \(\overrightarrow i ,\,\,\overrightarrow j ,\,\overrightarrow k\) lần lượt là các vectơ đơn vị trên các trục xOx’, yOy’, zOz’ với: \(\left | \vec{i} \right |=\left | \vec{j} \right |=\left | \vec{k} \right |=1.\)

Hệ trục như vậy được gọi là hệ trục tọa độ Oxyz, với O là gốc tọa độ.

b) Tọa độ của một điểm

Trong không gian Oxyz, cho điểm A tùy ý tồn tại duy nhất bộ số \((x_A,y_A,z_A)\) sao cho: \(A(x_A,y_A,z_A)\Leftrightarrow \overrightarrow{OA}=(x_A;y_A;z_A).\)

Bộ số \((x_A,y_A,z_A)\) được gọi là tọa độ điểm A.

c) Tọa độ của vectơ

Trong không gian Oxyz, cho vectơ \(\vec{u}\) tồn tại duy nhất bộ số \((x,y,z)\) sao cho: \(\overrightarrow{u}=(x;y;z)\)\(\Leftrightarrow \vec{u}=x\vec{i}+y\vec{j}+z\vec{k}.\)

Bộ số: \((x,y,z)\) được gọi là tọa độ của vectơ \(\vec{u}\).

2. Biểu thức tọa độ của các phép toán vectơ

Cho hai vectơ \(\vec{u}=(x;y;z)\) và \(\vec{u’}=(x’;y’; z’)\):

\(\vec{u}+\vec{u’}=(x+x’;y+y’;z+ z’)\)

\(\vec{u}-\vec{u’}=(x-x’;y-y’;z- z’)\)

\(k\vec{u}=(kx;ky;kz)\)

\(\vec{u}=u’\Leftrightarrow \left\{\begin{matrix} x=x’\\ y=y’\\ z=z’ \end{matrix}\right.\)

\(\vec{u}=\vec{u’}\) cùng phương \(\Leftrightarrow \left\{\begin{matrix} x=kx’\\ y=ky’\\ z=kz’ \end{matrix}\right.\)

\(\left | \vec{u} \right |=\sqrt{x^2+y^2+z^2}\)

Cho hai điểm \(A(x_A,y_A,z_A)\); \(B(x_B,y_B,z_B)\):

\(\overrightarrow{AB}=(x_B-x_A;y_B-y_A;z_B-z_A)\)

\(AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2}\)

\(\overrightarrow{IA}=k.\overrightarrow{IB}(k\neq 1)\Leftrightarrow \left\{\begin{matrix} x_I=\frac{x_A-k.x_B}{1-k}\\ \\ y_I=\frac{y_A-k.y_B}{1-k}\\ \\ z_I=\frac{z_A-k.z_B}{1-k} \end{matrix}\right.\)

Đặc biệt I là trung điểm AB thì: \(\left\{\begin{matrix} x_I=\frac{x_A+x_B}{2}\\ \\ y_I=\frac{y_A+y_B}{2}\\ \\ z_I=\frac{z_A+z_B}{2} \end{matrix}\right.\)

G là trọng tâm \(\Delta ABC\): \(\left\{\begin{matrix} x_G=\frac{x_A+x_B+x_C}{3}\\ \\ y_G=\frac{y_A+y_B+y_C}{3}\\ \\ z_G=\frac{z_A+z_B+z_C}{3} \end{matrix}\right.\)

G là trọng tâm của tứ diện ABCD: \(\left\{\begin{matrix} x_G=\frac{x_A+x_B+x_C+x_D}{4}\\ \\ y_G=\frac{y_A+y_B+y_C+y_D}{4}\\ \\ z_G=\frac{z_A+z_B+z_C+z_D}{4} \end{matrix}\right.\)

​3. Tích vô hướng

Công thức tính tích vô hướng:

\(\vec{a}.\vec{b}=\left | \vec{a} \right |.\left | \vec{b} \right |.cos(\vec{a},\vec{b})\).

Biểu thức tọa độ của tích vô hướng:

\(\left.\begin{matrix} \vec{a}=(x_1;y_1;z_1)\\ \vec{b}=(x_2;y_2;z_2) \end{matrix}\right\} \vec{a}.\vec{b} = x_1.x_2 + y_1.y_2 + z_1.z_2\).

Công thức tính góc giữa hai vectơ:

\(cos(\vec a,\vec b) = \frac{{\vec a.\vec b}}{{\left| {\vec a} \right|.\left| {\vec b} \right|}}.\)

4. Phương trình mặt cầu

Trong không gian Oxyz, mặt cầu tâm I(a;b;c), bán kính R có phương trình: \((x-a)^2+(y-b)^2+(z-c)^2=R^2.\)

Nhận xét:

Phương trình mặt cầu có thể viết dưới dạng \(x^2+y^2+z^2-2Ax-2By-2Cz+D=0\), điều kiện \(A^2+B^2+C^2-D> 0\).

Khi đó, mặt cầu có tâm \(I(A;B;C)\), bán kính \(R = \sqrt {{A^2} + {B^2} + {C^2} – D} .\)

Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong phần hoạt động của học sinh trên lớp sgk Hình học 12.

Câu hỏi

1. Trả lời câu hỏi 1 trang 63 sgk Hình học 12

Trong không gian \(Oxyz\), cho một điểm \(M\). Hãy phân tích vecto \(\overrightarrow {OM} \) theo ba vecto không đồng phẳng \(\overrightarrow i ;\,\overrightarrow j ;\,\overrightarrow k \) đã cho trên các trục \(Ox, Oy, Oz\).

Trả lời:

Ta có: \(\overrightarrow {OM}  = x\overrightarrow {i}  + y\overrightarrow {{\rm{j}}}  + z\overrightarrow {k} \)

2. Trả lời câu hỏi 2 trang 64 sgk Hình học 12

Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O, có \(\overrightarrow {AB} ;\,\overrightarrow {AD} ;\,\overrightarrow {{\rm{AA}}’} \) theo thứ tự cùng hướng với \(\overrightarrow i ;\,\overline j ;\,\overrightarrow k \) và có AB = a, AD = b, AA’ = c. Hãy tính tọa độ các vecto \(\overrightarrow {AB} ;\,\overrightarrow {AC} ;\,\overrightarrow {AC’} ;\,\overrightarrow {AM} \) với M là trung điểm của cạnh C’D’.

Trả lời:

Giả sử ta có hình vẽ như sau: (Chú ý vị trí các điểm trên hệ trục tọa độ)

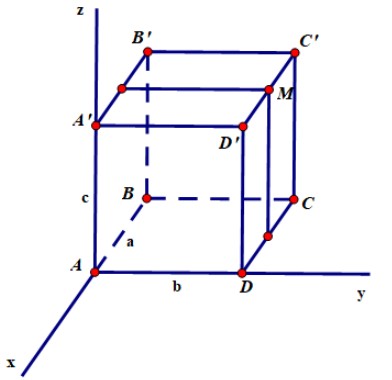
Từ hình vẽ trên ta có: \(A\left( {0;0;0} \right),B\left( {-a;0;0} \right),\) \(D\left( {0;b;0} \right), A’\left( {0;0;c} \right)\).

Suy ra \(C\left( {-a;b;0} \right),D’\left( {0;b;c} \right),\) \(B’\left( {-a;0;c} \right),C’\left( {-a;b;c} \right)\), \(M\left( {\dfrac{-a}{2};b;c} \right)\).

Vậy \(\overrightarrow {AB} = \left( {-a;0;0} \right),\) \(\overrightarrow {AC} = \left( {-a;b;0} \right),\) \(\overrightarrow {AC’} = \left( {-a;b;c} \right)\), \(\overrightarrow {AM} = \left( {\dfrac{-a}{2};b;c} \right)\).

3. Trả lời câu hỏi 3 trang 66 sgk Hình học 12

Với hệ tọa độ \(Oxyz\) trong không gian, cho \(\overrightarrow a = (3,0,1);\,\overrightarrow b = (1, – 1, – 2);\,\overrightarrow c = (2,1, – 1)\). Hãy tính \(\overrightarrow a .(\overrightarrow b + \overrightarrow c );\,\,|\overrightarrow a + \overrightarrow b |\)

Trả lời:

Ta có:

\(\overrightarrow b + \overrightarrow c = \left( {1 + 2; – 1 + 1;\left( { – 2} \right) + \left( { – 1} \right)} \right) = \left( {3;0; – 3} \right)\) \( \Rightarrow \overrightarrow a .\left( {\overrightarrow b + \overrightarrow c } \right) = 3.3 + 0.0 + 1.\left( { – 3} \right) = 6\)

\(\overrightarrow a + \overrightarrow b = \left( {3 + 1;0 + \left( { – 1} \right);1 + \left( { – 2} \right)} \right) = \left( {4; – 1; – 1} \right)\) \( \Rightarrow \left| {\overrightarrow a + \overrightarrow b } \right| = \sqrt {{4^2} + {{\left( { – 1} \right)}^2} + {{\left( { – 1} \right)}^2}} = \sqrt {18} = 3\sqrt 2 \)

4. Trả lời câu hỏi 4 trang 67 sgk Hình học 12

Viết phương trình mặt cầu tâm \(I(1; -2; 3)\) có bán kính \(r = 5\).

Trả lời:

Phương trình mặt cầu là: \({\left( {x – 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z – 3} \right)^2} = {5^2} = 25\)

Dưới đây là Hướng dẫn giải bài 1 2 3 4 5 6 trang 68 sgk Hình học 12. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập hình học 12 kèm bài giải chi tiết bài 1 2 3 4 5 6 trang 68 sgk Hình học 12 của Bài §1. Hệ tọa độ trong không gian trong Chương III. Phương pháp toạ độ trong không gian cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 6 trang 68 sgk Hình học 12
Giải bài 1 2 3 4 5 6 trang 68 sgk Hình học 12

1. Giải bài 1 trang 68 sgk Hình học 12

Cho ba vectơ \(\overrightarrow{a}\)(2; -5; 3), \(\overrightarrow{b}\)(0; 2; -1), \(\overrightarrow{c}\)(1; 7; 2).

a) Tính tọa độ của vectơ \(\overrightarrow{d}=4.\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+3\overrightarrow{c}\).

b) Tính tọa độ của vectơ \(\overrightarrow{e}=\overrightarrow{a}-4\overrightarrow{b}-2\overrightarrow{c}\).

Bài giải:

Ta có:

\(\begin{array}{l}a)\,\,\overrightarrow d = 4\overrightarrow a – \frac{1}{3}\overrightarrow b + 3\overrightarrow c \\\,\,\,\,\,\,\overrightarrow d = 4\left( {2; – 5;3} \right) – \frac{1}{3}\left( {0;2; – 1} \right) + 3\left( {1;7;2} \right)\\\,\,\,\,\,\,\overrightarrow d = \left( {8; – 20;12} \right) – \left( {0;\frac{2}{3}; – \frac{1}{3}} \right) + \left( {3;21;6} \right)\\\,\,\,\,\,\,\overrightarrow d = \left( {11;\frac{1}{3};\frac{{55}}{3}} \right)\\b)\,\,\overrightarrow e = \overrightarrow a – 4\overrightarrow b – 2\overrightarrow c \\\,\,\,\,\,\,\overrightarrow e = \left( {2; – 5;3} \right) – 4\left( {0;2; – 1} \right) – 2\left( {1;7;2} \right)\\\,\,\,\,\,\,\overrightarrow e = \left( {2; – 5;3} \right) – \left( {0;8; – 4} \right) – \left( {2;14;4} \right)\\\,\,\,\,\,\,\overrightarrow e = \left( {0; – 27;3} \right)\end{array}\)

2. Giải bài 2 trang 68 sgk Hình học 12

Cho ba điểm \(A = (1; -1; 1), B = (0; 1; 2), C = (1; 0; 1)\).

Tìm tọa độ trọng tâm \(G\) của tam giác \(ABC\).

Bài giải:

\(G\) là trọng tâm của tam giác ABC thì \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\) (*)

Giả sử \(G(x; y; z)\) thì \(\overrightarrow{GA} = (1 – x; -1 – y; 1 – z)\);

\(\overrightarrow{GB} = (-x; 1 – y; 2 – z)\);

\(\overrightarrow{GC} = (1 – x; -y; 1 – z)\);

⇒ \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC} = (2 – 3x; -3y; 4 – 3z)\)

Do hệ thức (*), ta có :

\(2 – 3x = 0 \Rightarrow x = \frac{2}{3}\) ;

\(-3y = 0 \Rightarrow y = 0\);

\( 4 – 3z = 0 \Rightarrow z = \frac{4}{3}\).

Vậy \(G(\frac{2}{3};0;\frac{4}{3})\).

Nhận xét: Trọng tâm \(G\) của tam giác \(ABC\) bằng trung bình cộng các tọa độ tương ứng của \(3\) đỉnh của tam giác.

\(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{1 + 0 + 1}}{3} = \frac{2}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{ – 1 + 1 + 0}}{3} = 0\\{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{{1 + 2 + 1}}{3} = \frac{4}{3}
\end{array} \right. \Rightarrow G\left( {\frac{2}{3};0;\frac{4}{3}} \right)\)

3. Giải bài 3 trang 68 sgk Hình học 12

Cho hình hộp \(ABCD.A’B’C’D’\) biết \(A = (1; 0; 1), B = (2; 1; 2), D = (1; -1; 1)\),

\(C’ (4; 5; -5)\). Tính tọa độ các đỉnh còn lại của hình hộp.

Bài giải:

Theo giả thiết ta có hình vẽ sau:

Ta có:

\(\eqalign{
& \overrightarrow {AB} = \left( {1;1;1} \right) \cr
& \overrightarrow {A{\rm{D}}} = \left( {0; – 1;0} \right) \cr
& \overrightarrow {BC} = \overrightarrow {A{\rm{D}}} \Leftrightarrow \left\{ \matrix{
{x_C} – 2 = 0 \hfill \cr
{y_C} – 1 = – 1 \hfill \cr
{z_C} – 2 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{x_C} = 2 \hfill \cr
{y_C} = 0 \hfill \cr
{z_C} = 2 \hfill \cr} \right. \cr} \)

Vậy \(C = (2; 0; 2)\)

Suy ra \(\overrightarrow {CC’} = \left( {2;5; – 7} \right)\)

Từ \(\overrightarrow {AA} = \overrightarrow {BB} = \overrightarrow {DD} = \overrightarrow {CC} = \left( {2;5; – 7} \right)\)

Suy ra

\(\left\{ \matrix{
{x_A} – 1 = 2 \hfill \cr
{y_A} – 0 = 5 \hfill \cr
{z_A} – 1 = – 7 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{x_A} = 3 \hfill \cr
{y_A} = 5 \hfill \cr
{z_A} = – 6 \hfill \cr} \right.\)

Vậy \(A’ (3; 5; -6)\)

Tương tự:

\(\begin{array}{l}\left\{ \begin{array}{l}{x_{B’}} – 2 = 2\\{y_{B’}} – 1 = 5\\{z_{B’}} – 2 = – 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{B’}} = 4\\{y_{B’}} = 6\\{z_{B’}} = – 5\end{array} \right. \Rightarrow B’\left( {4;6; – 5} \right)\\\left\{ \begin{array}{l}{x_{D’}} – 1 = 2\\{y_{D’}} + 1 = 5\\{z_{D’}} – 1 = – 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{D’}} = 3\\{y_{D’}} = 4\\{z_{D’}} = – 6\end{array} \right. \Rightarrow D’\left( {3;4; – 6} \right)\end{array}\)

4. Giải bài 4 trang 68 sgk Hình học 12

Tính:

a) \(\overrightarrow{a}.\overrightarrow{b}\) với \(\overrightarrow{a}(3; 0; -6)\), \(\overrightarrow{b}(2; -4; 0)\).

b) \(\overrightarrow{c}.\overrightarrow{d}\) với \(\overrightarrow{c}(1; -5; 2)\), \(\overrightarrow{d}(4; 3; -5)\).

Bài giải:

Ta có:

a) \(\overrightarrow{a}.\overrightarrow{b} = 3.2 + 0.(-4) +(-6).0 = 6\).

b) \(\overrightarrow{c}.\overrightarrow{d} = 1.4 + (-5).3 + 2.(-5) = -21\).

5. Giải bài 5 trang 68 sgk Hình học 12

Tìm tâm và bán kính của các mặt cầu có phương trình sau đây:

a) \({x^2} + {\rm{ }}{y^{2}} + {\rm{ }}{z^2}-{\rm{ }}8x{\rm{ }} – {\rm{ }}2y{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}0\) ;

b) \(3{x^2} + {\rm{ }}3{y^2} + {\rm{ }}3{z^2}-{\rm{ }}6x{\rm{ }} + {\rm{ }}8y{\rm{ }} + {\rm{ }}15z{\rm{ }}-{\rm{ }}3{\rm{ }} = {\rm{ }}0\).

Bài giải:

a) ♦ Cách 1:

Ta có phương trình:

\({x^2} + {\rm{ }}{y^{2}} + {\rm{ }}{z^2}-{\rm{ }}8x{\rm{ }} – {\rm{ }}2y{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}0\)

\( \Leftrightarrow {\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}4} \right)^2} + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}1} \right)^2} + {\rm{ }}{z^2} = {\rm{ }}{4^2}\)

Đây là mặt cầu tâm \(I(4; 1; 0)\) và có bán kính \(r = 4\).

♦ Cách 2:

Ta có: \(a = 4;\,\,b = 1;\,\,c = 0 ;\,\,d = 1 \Rightarrow {a^2} + {b^2} + {c^2} – d = 16 > 0\) do đó đây là phương trình mặt cầu tâm \(I\left( {4;1;0} \right)\), bán kính \(R=4\).

b) ♦ Cách 1:

Ta có phương trình:

\(3{x^2} + {\rm{ }}3{y^2} + {\rm{ }}3{z^2}-{\rm{ }}6x{\rm{ }} + {\rm{ }}8y{\rm{ }} + {\rm{ }}15z{\rm{ }}-{\rm{ }}3{\rm{ }} = {\rm{ }}0\)

\(\Leftrightarrow {x^2} + {y^2} + {z^2}{\rm{ – }}2x + {8 \over 3}y + 5z{\rm{ – }}1 = 0\)

\(⇔ (x-1)^{2}+(y+\frac{4}{3})^{2}+(z+\frac{5}{2})^{2}= (\frac{19}{6})^{2}\).

Đây là mặt cầu tâm \(J(1; -\frac{4}{3};-\frac{5}{2})\) và có bán kính là \(R = \frac{19}{6}\).

♦ Cách 2:

\(\begin{array}{l}\,\,\,\,\,\,3{x^2} + 3{y^2} + 3{z^2} – 6x + 8y + 15z – 3 = 0\\\Leftrightarrow {x^2} + {y^2} + {z^2} – 2x + \frac{8}{3}y + 5z – 1 = 0
\end{array}\)

Ta có: \(a = 1;\,\,b = – \frac{4}{3};\,\,c = – \frac{5}{2};\,\,d = – 1 \Rightarrow {a^2} + {b^2} + {c^2} – d = \frac{{336}}{{36}} > 0\) do đó đây là phương trình mặt cầu tâm \(J\left( {1; – \frac{4}{3}; – \frac{5}{2}} \right)\), bán kính \(R = \frac{{19}}{6}\).

6. Giải bài 6 trang 68 sgk Hình học 12

Lập phương trình mặt cầu trong hai trường hợp sau đây:

a) Có đường kính \(AB\) với \(A(4 ; -3 ; 7), B(2 ; 1 ; 3)\).

b) Đi qua điểm \(A = (5; -2; 1)\) và có tâm \(C(3; -3; 1)\).

Bài giải:

a) Gọi \(I\) là trung điểm của \(AB\), thì mặt cầu có đường kính \(AB\), có tâm \(I\) và bán kính \(r =\frac{1}{2}AB=IA\).

Ta có:

\(I (3; -1; 5)\) và \(r^2 = IA^2 = 9\).

Do vậy phương trình mặt cầu đường kính \(AB\) có dạng:

\({\left( {x{\rm{ }} – {\rm{ }}3} \right)^{2}} + {\rm{ }}{\left( {y{\rm{ }} + 1} \right)^2} + {\rm{ }}{\left( {z{\rm{ }}-{\rm{ }}5} \right)^2} = {\rm{ }}9\)

b) Mặt cầu cần tìm có tâm \(C(3; -3; 1)\) và có bán kính \(r = CA = \sqrt{4+1+0}=\sqrt{5}\)

Do đó phương trình mặt cầu có dạng:

\({\left( {x{\rm{ }} – {\rm{ }}3} \right)^2} + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}3} \right)^{2}} + {\rm{ }}{\left( {z{\rm{ }}-{\rm{ }}1} \right)^2} = {\rm{ }}5\).

Bài trước:

Bài tiếp theo:

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 12 với giải bài 1 2 3 4 5 6 trang 68 sgk Hình học 12!

“Bài tập nào khó đã có giaibaisgk.com“