Hướng dẫn Giải bài 1 2 3 4 5 trang 23 24 sgk Giải tích 12

Nội Dung

Hướng dẫn giải Bài §3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số, Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số, sách giáo khoa Giải tích 12. Nội dung bài giải bài 1 2 3 4 5 trang 23 24 sgk Giải tích 12 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập giải tích có trong SGK để giúp các em học sinh học tốt môn toán lớp 12.

Lý thuyết

1. Định nghĩa

Cho hàm số $y = f(x)$ xác định trên tập $D$.

– Số $M$ là giá trị lớn nhất (GTLN) của hàm số $f$ trên $D$

$⇔\left\{ \matrix{
f(x) \le M,\forall x \in D \hfill \cr
\exists {x_0} \in D\text{ sao cho }f({x_0}) = M \hfill \cr} \right.$

Kí hiệu : $M=\underset{D}{max} f(x).$

– Số $m$ là giá trị nhỏ nhất (GTNN) của hàm số $f$ trên $D$

$⇔\left\{ \matrix{
f(x) \ge m,\forall x \in D \hfill \cr
\exists {x_0} \in D\text{ sao cho }f({x_0}) = m \hfill \cr} \right.$

Kí hiệu: $m=\underset{D}{min} f(x).$

2. Cách tính GTLN và GTNN của hàm số trên một đoạn

Định lí:

Mọi hàm số liên tục trên một đoạn đều có GTLN và GTNN trên đoạn đó.

Quy tắc tìm GTLN, GTNN của hàm số y = f(x) liên tục trên đoạn [a ; b]

– Tìm các điểm x_i∈ (a ; b)(i = 1, 2, . . . , n) mà tại đó f'(x_i) = 0 hoặc f'(x_i) không xác định.

– Tính f(a), f(b), f(x_i) (i = 1, 2, . . . , n) .

– Khi đó: $\underset{[a;b]}{max} f(x)=\max \left \{ f(a); f(b); f(x_{i}) \right \}$;

$\underset{[a;b]}{min} f(x)=\min \left \{ f(a); f(b); f(x_{i}) \right \};$

Để tìm GTLN, GTNN của hàm số y=f(x) xác định trên tập hợp D, ta có thể khảo sát sự biến thiên của hàm số trên D, rồi căn cứ vào bảng biến thiên của hàm số mà kết luận về GTLN và GTNN của hàm số.

Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong phần hoạt động của học sinh sgk Giải tích 12.

Câu hỏi

1. Trả lời câu hỏi 1 trang 20 sgk Giải tích 12

Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:

a) $y = x^2$ trên đoạn $[-3; 0]$;

b) $y = \frac{ (x + 1)}{(x – 1)}$ trên đoạn $[3; 5]$.

Trả lời:

a) Ta có: $y’ = 2x ≤ 0$ trên đoạn $[-3; 0]$. Vậy hàm số nghịch biến trên đoạn $[-3,0]$.

Khi đó trên đoạn $[-3,0]$: hàm số đạt giá trị lớn nhất tại $x = -3$ và giá trị lớn nhất bằng $9$, hàm số đạt giá trị nhỏ nhất tại $x = 0$ và giá trị nhỏ nhất $= 0$.

b) Ta có: $y’ = – \frac{2}{(x-1)^2}$ < 0 trên đoạn $[3; 5]$. Vậy hàm số nghịch biến trên đoạn $[3; 5]$.

Khi đó trên đoạn $[-3,5]$: hàm số đạt giá trị lớn nhất tại $x = 3$ và giá trị lớn nhất bằng $2$, hàm số đạt giá trị nhỏ nhất tại $x = 5$ và giá trị nhỏ nhất $= 1.5$.

2. Trả lời câu hỏi 2 trang 21 sgk Giải tích 12

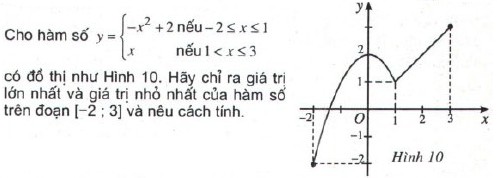
Trả lời:

Hàm số:

$y = \left\{ \matrix{
– {x^2} + 2\,;\,\, – 2 \le x \le 1 \hfill \cr
x\,\,;\,\,\,1 < x \le 3\,\, \hfill \cr} \right.$

Giá trị nhỏ nhất của hàm số trên đoạn $[-2, 3]$ là điểm thấp nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị nhỏ nhất tại $x = -2$. Thay $x = -2$ vào hàm số y đã cho ta có giá trị nhỏ nhất là $-2$.

Giá trị lớn nhất của hàm số trên đoạn $[-2,3]$ là điểm cao nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị lớn nhất tại $x = 3$. Thay $x = 3$ vào hàm số y đã cho ta có giá trị lớn nhất là $3$.

3. Trả lời câu hỏi 3 trang 23 sgk Giải tích 12

Lập bảng biến thiên của hàm số $f(x) = – \frac{1}{1 + x^2}$.

Từ đó suy ra giá trị nhỏ nhất của $f(x)$ trên tập xác định.

Trả lời:

– TXĐ: $D = R$.

$y’ = \frac{2x}{(1 + x^2)^2}$. Cho $y’ = 0$ thì $x = 0.$

– Bảng biến thiên:

Vậy giá trị nhỏ nhất của hàm số đã cho là $ -1$ tại $x = 0$.
Dưới đây là Hướng dẫn giải bài 1 2 3 4 5 trang 23 24 sgk Giải tích 12. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập giải tích 12 kèm bài giải chi tiết bài 1 2 3 4 5 trang 23 24 sgk Giải tích 12 của Bài §3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trong Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 trang 23 24 sgk Giải tích 12

1. Giải bài 1 trang 23 sgk Giải tích 12

Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:

a) $y = x^3 – 3x^2 – 9x + 35$ trên các đoạn $[-4; 4]$ và $[0;5]$.

b) $y = x^4 – 3x^2 + 2$ trên các đoạn $[0;3]$ và $[2;5]$.

c) $y =\frac{ (2-x)}{(1-x)}$ trên các đoạn $[2;4]$ và $[-3;-2]$.

d) $y =\sqrt{(5-4x)}$ trên đoạn $[-1;1]$.

Bài giải:

a) Xét hàm số $y = x^3 – 3x^2 – 9x + 35$

– Tập xác định $D=\mathbb{R}$.

– Hàm số liên tục trên các đoạn [-4;4] và [0;5] nên có GTLN và GTNN trên mỗi đoạn này.

Ta có: y’ = 3x² – 6x – 9 = 3(x² – 2x – 3)

♦ Trên đoạn [-4;4]:

$y’ = 0 \Leftrightarrow \left[ \begin{array}{l} x = 3 \in \left[ { – 4;4} \right]\\ x = – 1 \in \left[ { – 4;4} \right] \end{array} \right.$

Ta có: y(-4)=-41; y(4)=15; y(-1)=40; y(3)=8.

Vậy:

– Giá trị lớn nhất của hàm số là $\mathop {\max y}\limits_{x \in \left[ { – 4;4} \right]} = y( – 1) = 40$.

– Giá trị nhỏ nhất của hàm số là $\mathop {\min y}\limits_{x \in \left[ { – 4;4} \right]} = y( – 4) = – 41.$

♦ Trên đoạn [0;5]:

$y’ = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x = 3 \in \left[ {0;5} \right]}\\ {x = – 1 \notin \left[ {0;5} \right]} \end{array}} \right.$

Ta có: y(0)=35; y(5)=40; y(3)=8.

Vậy:

– Giá trị lớn nhất của hàm số là $\mathop {\max y}\limits_{x \in \left[ {0;5} \right]} = y(5) = 40.$

– Giá trị nhỏ nhất của hàm số là $\mathop {\min y}\limits_{x \in \left[ {0;5} \right]} = y(3) = 8.$

b) Xét hàm số $y = x^4 – 3x^2 + 2$

– Tập xác định $D=R$

– Hàm số liên tục trên các đoạn $[0;3]$ và $[2;5]$ nên có GTLN và GTNN trên các đoạn này:

– Đạo hàm: y’=4x³-6x.

♦ Trên đoạn [0;3]:

$y’ = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x = – \sqrt {\frac{3}{2}} \notin \left[ {0;3} \right]}\\ {x = 0 \in \left[ {0;3} \right]}\\ {x = \sqrt {\frac{3}{2}} \in \left[ {0;3} \right]} \end{array}} \right.$

Ta có: y(0)=2; $y\left( {\sqrt {\frac{3}{2}} } \right) = – \frac{1}{4}$; y(3)=56.

Vậy:

– Giá trị lớn nhất của hàm số:$\mathop {\max y}\limits_{x \in \left[ {0;3} \right]} = y\left( 3 \right) = 56.$

– Giá trị nhỏ nhất của hàm số: $\mathop {\min y}\limits_{x \in \left[ {0;3} \right]} = y\left( {\sqrt {\frac{3}{2}} } \right) = – \frac{1}{4}.$

♦ Trên đoạn [2;5]:

$y’ = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x = – \sqrt {\frac{3}{2}} \notin \left[ {2;5} \right]}\\ {x = 0 \notin \left[ {2;5} \right]}\\ {x = \sqrt {\frac{3}{2}} \notin \left[ {0;3} \right]} \end{array}} \right.$

Ta có: y(2)=6; y(5)=552

Vậy:

– Giá trị lớn nhất của hàm số $\mathop {\max y}\limits_{x \in \left[ {2;5} \right]} = y\left( 6 \right) = 552.$

– Giá trị nhỏ nhất của hàm số: $\mathop {\min y}\limits_{x \in \left[ {2;5} \right]} = y\left( 2 \right) = 6.$

c) Xét hàm số $y =\frac{ (2-x)}{(1-x)}$

Hàm số có tập xác định D = R \{1} và liên tục trên các đoạn [2;4] và [-3;-2] thuộc D, do đó hàm số có GTLN, GTNN trên mỗi đoạn này.

Ta có :

Ta có: $y’=\frac{1.\left( -1 \right)-1.\left( -2 \right)}{{{\left( x-1 \right)}^{2}}}=\frac{1}{{{\left( x-1 \right)}^{2}}}>0\ \ \forall x\ne 1.$

Với $D=\left[ 2;\ 4 \right]$ có: $y\left( 2 \right)=0;\ \ y\left( 4 \right)=\frac{2}{3}.$

Vậy $\underset{x\in \left[ 2;\ 4 \right]}{\mathop{\min }}\,y=0\ \ khi\ \ x=2$ và $\underset{x\in \left[ 2;\ 4 \right]}{\mathop{\max }}\,y=\frac{2}{3}\ \ khi\ \ x=4.$

♦ Trên đoạn [2;4]: $y(2)=0;y(4)=\frac{2}{3}.$

Vậy:

– Giá trị nhỏ nhất của hàm số: $\mathop {\min y}\limits_{x \in \left[ {2;4} \right]} = y\left( 2 \right) = 0.$

– Giá trị lớn nhất của hàm số: $\mathop {\max y}\limits_{x \in \left[ {2;4} \right]} = y\left( 4 \right) = \frac{2}{3}.$

♦ Trên đoạn [-3;-2]: $y(-3)=\frac{5}{4};y(-2)=\frac{4}{3}.$

Vậy:

– Giá trị nhỏ nhất của hàm số: $\mathop {\min y}\limits_{x \in \left[ { – 3;-2} \right]} = y\left( { – 3} \right) = \frac{5}{4}.$

– Giá trị lớn nhất của hàm số: $\mathop {\max y}\limits_{x \in \left[ { – 3; – 2} \right]} = y\left( { – 2} \right) = \frac{4}{3}.$

d) Xét hàm số $y =\sqrt{(5-4x)}$

Hàm số có tập xác định ${\rm{D = }}\left( { – \infty ;\frac{5}{4}} \right]$ nên xác định và liên tục trên đoạn [-1;1], do đó có GTLN, GTNN trên đoạn [-1;1].

Ta có:$y’ = – \frac{2}{{\sqrt {5 – 4x} }} < 0,\forall x \in \left[ { – 1;1} \right].$

♦ Trên đoạn [-1;1]: y(-1)=3; y(1)=1.

Vậy:

– Giá trị lớn nhất của hàm số $\mathop {\max }\limits_{x \in \left[ { – 1;1} \right]} y = y( – 1) = 3.$

– Giá trị nhỏ nhất của hàm số $\mathop {\min }\limits_{x \in \left[ { – 1;1} \right]} y = y(1) = 1.$

2. Giải bài 2 trang 24 sgk Giải tích 12

Trong số các hình chữ nhật cùng có chu vi 16 cm, hãy tìm hình chữ nhật có diện tích lớn nhất.

Bài giải:

♦ Cách 1: Áp dụng bất đăng thức cô-si

Kí hiệu $x, y$ thứ tự là chiều dài và chiều rộng của hình chữ nhật $(0 < x, y < 16)$.

Khi đó $x + y = 8$.

Theo bất đẳng thức Cô-si, ta có: $8=x+y\geq 2 \sqrt {x.y}\Rightarrow xy\leq 16.$

$xy=16\Leftrightarrow x=y=4.$

Vậy diện tích hình chữ nhật lớn nhất bằng $16 cm^2$ khi $x = y = 4(cm)$, tức là khi hình chữ nhật là hình vuông.

♦ Cách 2: Ứng dụng đạo hàm để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Gọi $x, y$ lần lượt là chiều dài và chiều rộng của hình chữ nhật $(8>x>0; 8>y>0)$.

Khi đó chu vi: $p=2(x+y)=16 ⇔ x+y=8 ⇔ y=8-x.$

Ta có diện tích của hình chữ nhật là:

$S=x.y=x(8-x) ⇔ S=-x^2 + 8x$.

Xét hàm số: $S(x) = -x$2 + 8x$ trên khoảng $(0, 8)$ ta có:

$S’=-2x + 8; S’= 0 ⇔ x=4$

Bảng biến thiên:

Từ bảng biến thiên ta thấy hàm số đạt giá trị lớn nhất tại x=4 khi đó maxS = 16.

Với $x=4$ suy ra $y=4$.

Vậy hình vuông có cạnh bằng $4$ là hình có diện tích lớn nhất.

3. Giải bài 3 trang 24 sgk Giải tích 12

Trong tất cả các hình chữ nhật cùng có diện tích $48 m^2$, hãy xác định hình chữ nhật có chu vi nhỏ nhất.

Bài giải:

♦ Cách 1: Sử dụng bất đẳng thức cô-si:

♦ Cách 2: Ứng dụng đạo hàm để tìm giá trị lớn nhất và nhỏ nhất của hàm số

Gọi x,y lần lượt là chiều dài và chiều rộng của hình chữ nhật (x>0,y>0)

Ta có:

Khi đó chu vi của hình chữ nhật là $p=2(x+y) \Leftrightarrow p=2x+\frac{96}{x}.$

Xét hàm số $P\left( x \right)=2\left( x+\dfrac{48}{x} \right)$ trên $\left( 0;+\infty \right)$ ta có:

$\begin{array}{l}
P’\left( x \right) = 2\left( {1 – \dfrac{{48}}{{{x^2}}}} \right) \Rightarrow P’\left( x \right) = 0 \Leftrightarrow {x^2} – 48 = 0\\
\Leftrightarrow {x^2} = 48 \Leftrightarrow \left[ \begin{array}{l}
x = 4\sqrt 3 \; \in \left( {0; + \infty } \right)\\
x = – 4\sqrt 3 \;\; \notin \left( {0; + \infty } \right)
\end{array} \right..
\end{array}$

Ta có: $P\left( 4\sqrt{3} \right)=16\sqrt{3}.$

$\begin{align} & \underset{x\to 0}{\mathop{\lim }}\,P\left( x \right)=\underset{x\to 0}{\mathop{\lim }}\,\ 2\left( x+\dfrac{48}{x} \right)=+\infty . \\ & \underset{x\to +\infty }{\mathop{\lim }}\,P\left( x \right)=\underset{x\to +\infty }{\mathop{\lim }}\,\ 2\left( x+\dfrac{48}{x} \right)=+\infty . \\ & \Rightarrow Min\ P\left( x \right)=16\sqrt{3}\ \ khi\ \ x=4\sqrt{3}. \\ & \Rightarrow y=\dfrac{48}{4\sqrt{3}}=4\sqrt{3}m. \\ \end{align}$

Bảng biến thiên:

Từ bảng biến thiên ta có: $\min p = 16\sqrt 3$ khi $x = 4\sqrt 3 \,$.

Với $x = 4\sqrt 3 \,\Rightarrow y=\frac{48}{x}=4\sqrt 3$.

Vậy hình vuông có cạnh $4\sqrt 3 \,$ là hình có chu vi nhỏ nhất theo yêu cầu bài toán.

4. Giải bài 4 trang 24 sgk Giải tích 12

Tính giá trị lớn nhất của các hàm số sau:

a) $y=\frac{4}{1+x^2}$.

b) $y=4x^3-3x^4$.

Bài giải:

a) $y=\frac{4}{1+{{x}^{2}}}.$

Tập xác định: $D=R.$

Ta có: $y’=\frac{-2x.4}{{{\left( 1+{{x}^{2}} \right)}^{2}}}=\frac{-8x}{{{\left( 1+{{x}^{2}} \right)}^{2}}}\Rightarrow y’=0\Leftrightarrow 8x=0\Leftrightarrow x=0.$

$\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{4}{1+{{x}^{2}}}=0.$

Ta có bảng biến thiên:

Từ bảng biến thiên ta thấy hàm số đạt GTLN tại $x=0;\ \ \underset{R}{\mathop{\max }}\,y=4.$

b) $y=4{{x}^{3}}-3{{x}^{4}}.$

Tập xác định: $D=R.$

Ta có: $y’=12{{x}^{2}}-12{{x}^{3}}\Rightarrow y’=0\Leftrightarrow 12{{x}^{2}}-12{{x}^{3}}=0\Leftrightarrow \left[ \begin{align}& x=0 \\ & x=1 \\ \end{align} \right..$

$\underset{x\to \pm \infty }{\mathop{\lim }}\,y=\underset{x\to \pm \infty }{\mathop{\lim }}\,\left( 4{{x}^{3}}-3{{x}^{4}} \right)=-\infty .$

Ta có bảng biến thiên:

Theo bảng biến thiên ta thấy hàm số đạt GTLN tại $x=1;\ \ \underset{R}{\mathop{\max }}\,y=1.$

5. Giải bài 5 trang 24 sgk Giải tích 12

Tính giá trị nhỏ nhất của các hàm số sau:

a) $y = \left | x \right |$;

b) $y = x+\frac{4}{x} ( x > 0)$

Bài giải:

a) $y=\left| x \right|.$

Ta có: y = |x| ≥ 0 ∀ x

Tập xác định: $D=R.$

Ta có bảng biến thiên:

Từ bảng biến thiên ta có hàm số đạt GTNN tại $x=0;\ \underset{R}{\mathop{\min }}\,=0.$

b) $y=x+\frac{4}{x}\ \ \ \left( x>0 \right).$

Ta có: $y’=1-\frac{4}{{{x}^{2}}}\Rightarrow y’=0\Leftrightarrow 1-\frac{4}{{{x}^{2}}}=0\Leftrightarrow {{x}^{2}}-4=0\Leftrightarrow \left[ \begin{align}& x=-2\notin \left( 0;+\infty \right) \\ & x=2\in \left( 0;+\infty \right) \\ \end{align} \right..$

Bảng biến thiên:

Từ bảng biến thiên ta thấy: $\underset{\left( 0;+\infty \right)}{\mathop{Min}}\,y=4\ \ khi\ \ x=2.$

Bài trước:

Giải bài 1 2 3 4 5 6 trang 18 sgk Giải tích 12

Bài tiếp theo:

Giải bài 1 2 trang 30 31 sgk Giải tích 12

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 12 với giải bài 1 2 3 4 5 trang 23 24 sgk Giải tích 12!

“Bài tập nào khó đã có giaibaisgk.com“