Nội Dung
Hướng dẫn giải Bài §4. Hàm số mũ. Hàm số lôgarit, Chương 2. Hàm số lũy thừa. Hàm số mũ và Hàm số lôgarit, sách giáo khoa Giải tích 12. Nội dung bài giải bài 1 2 3 4 5 trang 78 79 sgk Giải tích 12 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập giải tích có trong SGK để giúp các em học sinh học tốt môn toán lớp 12.
Lý thuyết
1. Hàm số mũ
a) Định nghĩa hàm số mũ
Cho số thực dương \(a\) khác $1$.
Hàm số \(y=a^x\) được gọi là hàm số mũ cơ số \(a\).
b) Tính chất hàm số mũ
– Tập xác định: \(\mathbb{R}.\)
– Tập giá trị: \((0;+\infty )\)
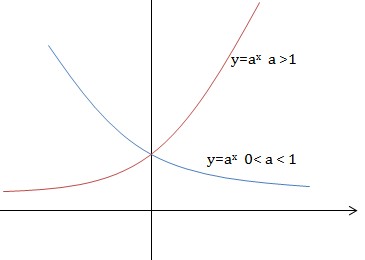
Với \(a>1\) hàm số \(y=a^x\) đồng biến trên \(\mathbb{R}.\)
Với $0< a < 1$ thì hàm số luôn nghịch biến
– Đồ thị hàm số mũ nhận trục \(Ox\) làm tiệm cận ngang.
c) Đạo hàm của hàm số mũ
Hàm số \(y=e^x\) có đạo hàm với mọi \(x\) và: \(\left ( e^x \right )’=e^x\)
Hàm số \(y=a^x(a>0,a\ne 1)\) có đạo hàm tại mọi \(x\) và: \(\left( {{a^x}} \right)’ = {a^x}{\mathop{\rm lna}\nolimits}\)
Đối với hàm hợp:
\(({e^u})’ = u’.{e^u}\)
\(({a^u})’ = {a^u}.\ln a.u’\)
2. Hàm số Lôgarit
a) Định nghĩa hàm số Lôgarit
Cho số thực dương \(a\) khác $1$.
Hàm số \(y=\log_ax\) được gọi là hàm số lôgarit cơ số \(a.\)
b) Tính chất hàm số Lôgarit
– Tập xác định: \(\left( {0; + \infty } \right).\)
– Tập giá trị: \(\mathbb{R}.\)
Với \(a>1\): \(y=\log_ax\) là hàm số đồng biến trên \(\left( {0; + \infty } \right).\)
Với 0< a < 1 thì hàm số luôn nghịch biến
Với \(x_1>0,x_2>0\): \(\log_ax_1=\log_ax_2\Leftrightarrow x_1=x_2\)
c) Đạo hàm của hàm số logarit
\(\left( {{{\log }_a}x} \right)’ = \frac{1}{{x\ln a}}\)
\(\left( {{{\log }_a}\left| x \right|} \right)’ = \frac{1}{{x\ln a}}\)
\(\left( {\ln x} \right)’ = \frac{1}{x}\)
Đối với hàm hợp:
\(\left( {{{\log }_a}u} \right)’ = \frac{{u’}}{{u.\ln a}}\)
\(\left( {\ln u} \right)’ = \frac{{u’}}{{\ln u}}\)
Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong phần hoạt động của học sinh sgk Giải tích 12.
Câu hỏi
1. Trả lời câu hỏi 1 trang 72 sgk Giải tích 12
Cho biết năm $2003$, Việt Nam có $80902400$ người và tỉ lệ tăng dân số là $1,47$%. Hỏi năm $2010$ Việt Nam sẽ có bao nhiêu người, nếu tỉ lệ tăng dân số hằng năm không đổi?
Trả lời:
Từ năm $2003$ đến năm $2010$ là $7$ năm.
Do đó năm $2010$ Việt Nam sẽ có số người là:
$80902400.(1 + 0.0147)^7 = 89603511,14$.
2. Trả lời câu hỏi 2 trang 72 sgk Giải tích 12
Trong các hàm số sau đây, hàm số nào là hàm số mũ ? Với cơ số bao nhiêu ?
\(\eqalign{
& a)\,y = {(\sqrt 3 )^x} \cr
& b)\,y = {5^{{x \over 3}}} \cr
& c)\,y = {x^{ – 4}} \cr
& d)y = {4^{ – x}} \cr} \)
Trả lời:
Các hàm số mũ là \(y = {(\sqrt 3 )^x}\) với cơ số là \(\sqrt 3 \); \(y = {5^{{x \over 3}}}\) với cơ số là \({5^{{1 \over 3}}}\); \(y = {4^{ – x}}\) với cơ số là \({4^{ – 1}}\)
3. Trả lời câu hỏi 3 trang 76 sgk Giải tích 12
Tìm đạo hàm của hàm số: \(y = \ln (x + \sqrt {(1 + {x^2})} )\)
Trả lời:
Ta có:
\(\eqalign{
& y’ = {\rm{[}}\ln (x + \sqrt {1 + {x^2}} ){\rm{]’}} \cr
& {\rm{ = }}{{(x + \sqrt {1 + {x^2}} )’} \over {x + \sqrt {1 + {x^2}} }} = {{1 + {x \over {\sqrt {1 + {x^2}} }}} \over {x + \sqrt {1 + {x^2}} }} = {1 \over {\sqrt {1 + {x^2}} }} \cr} \)
4. Trả lời câu hỏi 4 trang 78 sgk Giải tích 12
Nêu nhận xét về mối liên hệ giữa đồ thị của các hàm số trên Hình 35 và Hình 36.

Trả lời:
Nhận xét: Đồ thị của các hàm số trên Hình 35 và Hình 36 đối xứng nhau qua đường thẳng $y = x$.
Dưới đây là Hướng dẫn giải bài 1 2 3 4 5 trang 78 79 sgk Giải tích 12. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập giải tích 12 kèm bài giải chi tiết bài 1 2 3 4 5 trang 78 79 sgk Giải tích 12 của Bài §4. Hàm số mũ. Hàm số lôgarit trong Chương 2. Hàm số lũy thừa. Hàm số mũ và Hàm số lôgarit cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 1 trang 78 sgk Giải tích 12
Vẽ đồ thị của các hàm số sau:
a) $y=4^{x}$ ; b) $y=\frac{1}{4}^{x}$
Bài giải:
a) Hàm số \(y = 4^x\)
– Tập xác định: \(\mathbb R\)
– Sự biến thiên:
\(y’ = {4^x}\ln 4 > 0,\forall x \in \mathbb R\)
Hàm số đồng biến trên \(\mathbb R\)
– Giới hạn đặc biệt:
\(\eqalign{
& \mathop {\lim }\limits_{x \to – \infty } y = 0 \cr
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty \cr} \)
Tiệm cận ngang: \(y=0\).
– Bảng biến thiên:

– Đồ thị: Đồ thị nằm hoàn toàn phía trên trục hoành, cắt trục tung tại các điểm \((0;1)\), đi qua điểm \((1;4)\) và qua các điểm \((\frac{1}{2}; 2)\), \((-\frac{1}{2}; \frac{1}{2})\), \((-1; \frac{1}{4})\).

b) Hàm số \(y=\left ( \frac{1}{4} \right )^{x}\)
– Tập xác định: \(\mathbb R\)
– Sự biến thiên:
\(y’ = {\left( {\frac{1}{4}} \right)^x}.\ln \left( {\frac{1}{4}} \right) = – {\left( {\frac{1}{4}} \right)^x}\ln 4 < 0\,\,\forall x \in R\)
Hàm số nghịch biến trên \(\mathbb R\)
– Giới hạn:
\(\eqalign{
& \mathop {\lim }\limits_{x \to – \infty } y = + \infty \cr
& \mathop {\lim }\limits_{x \to + \infty } y = 0 \cr} \)
Tiệm cận ngang \(y=0\)
– Bảng biến thiên:

Đồ thị: Đồ thị hàm số nằm hoàn toàn về phía trên trục hoành, cắt trục tung tại điểm $(0; 1)$, đi qua điểm $(1; \frac{1}{4})$ và qua các điểm$(-\frac{1}{2}; 2), (-1;4)$.

2. Giải bài 2 trang 78 sgk Giải tích 12
Tính đạo hàm của các hàm số:
a) $y=2xe^{x}+3\sin 2x$;
b) $y=5x^{2}+2^{x}\cos x$;
c) $y=\frac{x+1}{3^{x}}$ .
Bài giải:
a) Ta có:
\(y’ = (2x{e^x})’ + 3(\sin 2x)’ \)
\(= 2.{e^x} + 2x({e^x})’+ {\rm{ }}3.2cos2x\)
\(=2\left( {1 + x} \right){e^x} + 6cos2x\)
b) Ta có:
\(\begin{array}{l}y’ = 5.2x – \left( {\left( {{2^x}} \right)’.\cos x + {2^x}.\left( {\cos x} \right)’} \right)\\\,\,\,\,\,\, = 10x – \left( {{2^x}.\ln 2.\cos x – {2^x}.\sin x} \right)\\\,\,\,\,\,\, = 10x – {2^x}\left( {\ln 2\cos x – \sin x} \right)\end{array}\)
c) Ta có:
\(\begin{array}{l}y’ = \frac{{\left( {x + 1} \right)'{{.3}^x} – \left( {x + 1} \right).\left( {{3^x}} \right)’}}{{{{\left( {{3^x}} \right)}^2}}}\\\,\,\,\,\, = \frac{{{3^x} – \left( {x + 1} \right){{.3}^x}\ln 3}}{{{{\left( {{3^x}} \right)}^2}}}\\\,\,\,\, = \frac{{{3^x}\left( {1 – \left( {x + 1} \right)\ln 3} \right)}}{{{{\left( {{3^x}} \right)}^2}}}\\\,\,\,\, = \frac{{1 – \left( {x + 1} \right)\ln 3}}{{{3^x}}}\end{array}\)
3. Giải bài 3 trang 78 sgk Giải tích 12
Tìm tập xác định của các hàm số:
a) $y=\log_{2}(5-2x)$;
b) $y=\log_{3}(x^{2}-2x)$;
c) $y=\log_{\frac{1}{5}}(x^{2}-4x+3)$;
d) $y=\log_{0,4}\frac{3x+2}{1-x}$.
Bài giải:
a) Hàm số \(y = lo{g_2}\left( {5 – 2x} \right)\) xác định khi và chỉ khi:
\[5- 2x > 0\Leftrightarrow x < \dfrac{5}{2}.\]
Vậy hàm số \(y = lo{g_2}\left( {5 – 2x} \right)\) có tập xác định là \(D=\left( \displaystyle{ – \infty ;{5 \over 2}} \right).\)
b) Hàm số \(y =lo{g_3}({x^2} – 2x)\) xác định khi và chỉ khi:
\[{x^2} – 2x > 0 \Leftrightarrow \left[ \begin{array}{l}
x > 2\\
x < 0
\end{array} \right.\]
Vậy hàm số \(y =lo{g_3}({x^2} – 2x)\) có tập xác định là \(D=(-∞; 0) ∪ (2;+∞)\).
c) Hàm số \(y=log_{\frac{1}{5}}\left ( x^{2} -4x+3 \right )\) xác định khi và chỉ khi
\[{x^2} – 4x + 3 > 0 \Leftrightarrow \left[ \begin{array}{l}
x > 3\\
x < 1
\end{array} \right.\]
Vậy hàm số \(y= log_{\frac{1}{5}}\left ( x^{2} -4x+3 \right )\) có tập xác định là \(D=(-∞; 1) ∪ (3;+∞)\).
d) Hàm số \(y= log_{0,4}\dfrac{3x+2}{1-x}\) xác định khi và chỉ khi:
\(\dfrac{3x+2}{1-x} > 0\Leftrightarrow (3x+2) (1-x) > 0\) \(\Leftrightarrow-\dfrac{2}{3} < x <1.\)
Hoặc
$\left\{\begin{matrix}3x+2>0 & \\ 1-x>0 & \end{matrix}\right.⇔ \left\{\begin{matrix}x>-\frac{2}{3} & \\ x<1 & \end{matrix}\right.$
Bảng xét dấu:

Vậy hàm số \(y = log_{0,4}\dfrac{3x+1}{1-x}\) có tập xác định là \(D=\left( \displaystyle{ – {2 \over 3};1} \right)\).
4. Giải bài 4 trang 79 sgk Giải tích 12
Vẽ đồ thị của các hàm số:
a) $y=\log x$ ;
b) $y=\log _{\frac{1}{2}}x$
Bài giải:
a) Đồ thị hàm số \(y = logx\).
– Tập xác định: \(D=(0;+\infty)\)
– Sự biến thiên:
\(y’ = {1 \over {x\ln 10}} > 0,\forall x \in D\)
Hàm số đồng biến trên khoảng \((0;+\infty)\)
– Giới hạn đặc biệt:
\(\eqalign{
& \mathop {\lim }\limits_{x \to {0^ + }} y = – \infty \cr
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty \cr} \)
Hàm số có tiệm cận đứng là: \(x=0\)
– Bảng biến thiên:

– Đồ thị: Đồ thị hàm số nằm hoàn toàn bên phải trục tung) nhận trục tung làm tiệm cận đứng, cắt trục hoành tại điểm \((1;0)\) và đi qua điểm \((10;1)\), \((\frac{1}{10}; -1)\).

b) Đồ thị hàm sốy = \(log_{\frac{1}{2}}x\).
– Tập xác định: \(D=(0;+\infty)\)
– Sự biến thiên:
\(y’ = – {1 \over {x\ln 2}} < 0,\forall x \in D\)
Hàm số nghịch biến trên khoảng \((0;+\infty)\)
– Giới hạn:
\(\eqalign{
& \mathop {\lim }\limits_{x \to {0^ + }} y = + \infty \cr
& \mathop {\lim }\limits_{x \to + \infty } y = – \infty \cr} \)
Hàm số có tiệm cận đứng \(x=0\).
– Bảng biến thiên:

– Đồ thị: Đồ thị hàm số nằm hoàn toàn bên phải trục tung (nhận trục tung làm tiệm cận đứng), cắt trục hoành tại điểm \((1;0)\) và đi qua điêm \((\frac{1}{2};1)\), điểm phụ \((2;-1)\), \((4.-2)\), \((\frac{1}{4}; 2)\).

5. Giải bài 5 trang 79 sgk Giải tích 12
Tính đạo hàm của các hàm số:
a) $y= 3x^{2} – \ln x + 4 \sin x$;
b) $y= \log (x^{2}+ x + 1)$;
c) $y=\frac{\log _{3}x}{x}$.
Bài giải:
a) $y= 3x^{2} – \ln x + 4 \sin x$
⇒ $y’=( 3x^{2} – \ln x + 4 \sin x)’=( 3x^{2})’ – (\ln )’ +(4 \sin x)’$
⇒ $y’=6x – \frac{1}{x} + 4 \cos x$
b) $y= \log (x^{2}+ x + 1)$
⇒ $y’= (\log (x^{2}+ x + 1))’$
⇒ $y’=\frac{(x^{2}+x+1)’}{(x^{2}+x+1)\ln 10}$
⇒ $y’=\frac{2x+1}{(x^{2}+x+1)\ln 10}$
c) $y=\frac{\log _{3}x}{x}$
⇒ $y’=(\frac{\log _{3}x}{x})’$
⇒ $y’=\frac{x(\log_{3}x)’-x’.(\log_{3}x)}{x^{2}}$
⇒ $y’=\frac{\frac{x}{x\ln x}-\log_{3}x}{x^{2}}$
⇒ $y’=\frac{1-\ln x}{x^{2}\ln 3}$
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 12 khác
- Để học tốt môn Vật lí lớp 12
- Để học tốt môn Sinh học lớp 12
- Để học tốt môn Ngữ văn lớp 12
- Để học tốt môn Lịch sử lớp 12
- Để học tốt môn Địa lí lớp 12
- Để học tốt môn Tiếng Anh lớp 12
- Để học tốt môn Tiếng Anh lớp 12 thí điểm
- Để học tốt môn Tin học lớp 12
- Để học tốt môn GDCD lớp 12
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 12 với giải bài 1 2 3 4 5 trang 78 79 sgk Giải tích 12!
“Bài tập nào khó đã có giaibaisgk.com“
