Hướng dẫn Giải bài 1 2 3 4 trang 105 sgk Đại số 10

Nội Dung

Hướng dẫn giải Bài §5. Dấu của tam thức bậc hai, Chương IV. Bất đẳng thức. Bất phương trình, sách giáo khoa Đại số 10. Nội dung bài giải bài 1 2 3 4 trang 105 sgk Đại số 10 cơ bản bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập đại số có trong SGK để giúp các em học sinh học tốt môn toán lớp 10.

Lý thuyết

I. Định lí về dấu của tam thức bậc hai

1. Tam thức bậc hai

Tam thức bậc hai đối với x là biểu thức có dạng $f(x)=ax^2+bx+c$ trong đó a, b, c là những hệ số, $a \neq 0$

2. Dấu của tam thức bậc hai

ĐỊNH LÍ: Cho $f(x)=ax^2+bx+c\,(a\neq 0), \Delta = b^2-4ac$

Nếu $\Delta <0$ thì $f(x)$ luôn cùng dấu với hệ số $a, \forall x \in \mathbb{R}$

Nếu $\Delta =0$ thì $f(x)$ luôn cùng dấu với hệ số a trừ khi $x=-\frac{-b}{2a}$

Nếu $\Delta >0$ thì $f(x)$ cùng dấu với hệ số a khi $x<x_1$hoặc $x>x_2$, trái dấu với hệ số a khi $x_1<x<x_2$ trong đó $x_1; x_2\,(x_1<x_2)$ là hai nghiệm của $f(x)$.

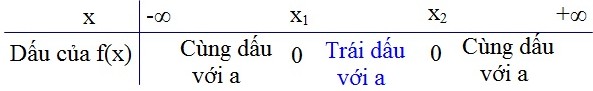
Chú ý:

Cũng như khi giải phương trình bậc hai, khi xét dấu tam thức bậc hai, ta có thể dùng biểu thức thu gọn $\Delta ‘$ thay cho $\Delta $ và cũng được các kết quả tương tự.

Ví dụ: $f(x) = 2{x^2} – x + 1 > 0$ với mọi $x \in R$ vì tam thức f(x) có$ \Delta = – 7 < 0$ và a = 2 > 0

Nhận xét:

Từ định lý về dấu của tam thức bậc hai, ta thấy chỉ có một trường hợp duy nhất trong đó dấu của tam thức không thay đổi ( luôn âm hoặc luôn dương), đó là khi $\Delta < 0$. Lúc đó, dấu của tam thức trùng với dấu của hệ số a. với $\Delta = b^2-4ac$.

Ta có:

$f(x) >0 \quad \forall x \in \mathbb{R} \Leftrightarrow \begin{cases}\Delta <0 \\ a>0\end{cases}$

$f(x) <0 \quad \forall x \in \mathbb{R} \Leftrightarrow \begin{cases} \Delta <0 \\ a<0 \end{cases}$

$f(x) \ge 0 \quad \forall x \in \mathbb{R} \Leftrightarrow \begin{cases} \Delta \le 0 \\ a>0 \end{cases}$

$f(x) \le 0 \quad \forall x \in \mathbb{R} \Leftrightarrow \begin{cases} \Delta \le 0 \\ a<0 \end{cases}$

II. Bất phương trình bậc hai một ẩn

1. Bất phương trình bậc hai

Bất phương trình bậc nhất hai ẩn x là bất phương trình dạng $ax^2+bx+c<0$ (hoặc $ax^2+bx+c>0; ax^2+bx+c \geq 0; ax^2+bx+c \leq 0$ trong đó a, b, c là những số thực đã cho, $a \neq 0$

2. Giải bất phương trình bậc hai

Giải bất phương trình bậc hai $ax^2+bx+c<0$ thực chất là tìm các khoảng mà trong đó $f(x)=ax^2+bx+c$ cùng dấu với hệ số a (trường hợp a < 0) hay trái dấu với hệ số a (trường hợp a > 0).

Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong phần hoạt động của học sinh sgk Đại số 10.

Câu hỏi

1. Trả lời câu hỏi 1 trang 100 sgk Đại số 10

1) Xét tam thức bậc hai $f(x) = $x² $– 5x + 4$. Tính $f(4), f(2), f(-1), f(0)$ và nhận xét về dấu của chúng.

2) Quan sát đồ thị hàm số $y = $x² $– 5x + 4$ (h.32a)) và chỉ ra các khoảng trên đó đồ thị ở phía trên, phía dưới trục hoành.

3) Quan sát các đồ thị trong hình 32 và rút ra mối liện hệ về dấu của giá trị $f(x) =$ ax²+$ bx + c$ ứng với $x$ tùy theo dấu của biệt thức $Δ = $b² $– 4ac.$

Trả lời:

1) $f(x) = $x² $– 5x +4$

⇒ $f(4)= 0;$ $f(2) = -2 < 0;$

$f(-1)= 10 > 0;$ $f(0) = 4 > 0.$

2) Với $1 < x < 4$ thì đồ thị nằm phía dưới trục hoành.

Với $x < 1$ hoặc $x > 4$ thì đồ thị nằm phía trên trục hoành.

3) Hình 32a) có $Δ > 0 ⇒ f(x)$ cùng dấu với $a$ khi $x$ nằm ngoài khoảng hai nghiệm của phương trình $f(x) = 0; f(x)$ trái dấu với $a$ khi $x$ nằm trong khoảng hai nghiệm của phương trình $f(x) = 0.$

Hình 32b) có $Δ = 0 ⇒ f(x)$ cùng dấu với $a$, trừ khi $x = – b/2a.$

Hình 32c) có $Δ < 0 ⇒ f(x)$ cùng dấu với $a.$

2. Trả lời câu hỏi 2 trang 103 sgk Đại số 10

Xét dấu các tam thức

a) $f(x) =$ 3x² $+ 2x – 5;$

b) $g(x) =$ 9x² $– 24x + 16.$

Trả lời:

a) $f(x) =$ 3x² $+ 2x – 5$ có hai nghiệm phân biệt $x = 1; x = -5/3$, hệ số $a = 3 >0.$

Ta có bảng xét dấu $f(x)$ như sau:

b) $g(x) =$ 9x² $– 24x + 16$ = (3x – 4)² $> 0 ∀x.$

Vậy $g(x) > 0 ∀x.$

3. Trả lời câu hỏi 3 trang 103 sgk Đại số 10

Trong các khoảng nào

a) $f(x) = $-2x² $+ 3x + 5$ trái dấu với hệ số của x² ?

b) $g(x) = $-3x² $+ 7x – 4$ cùng dấu với hệ số của x² ?

Trả lời:

a) Với $-1 < x < 5/2$ thì $f(x)$ trái dấu với hệ số của x²

b) Với $x < 1$ hoặc $x > 4/3$ thì $g(x)$ cùng dấu với hệ số của x²

Dưới đây là phần Hướng dẫn giải bài 1 2 3 4 trang 105 sgk Đại số 10 cơ bản. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập đại số 10 kèm bài giải chi tiết bài 1 2 3 4 trang 105 sgk Đại số 10 cơ bản của Bài §5. Dấu của tam thức bậc hai trong Chương IV. Bất đẳng thức. Bất phương trình cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 trang 105 sgk Đại số 10

1. Giải bài 1 trang 105 sgk Đại số 10

Xét dấu các tam thức bậc hai

a) ${x^{2}}-3x + 1$;

b) $- 2{x^2} + 3x + 5$;

c) ${x^2} +12x+36$;

d) $(2x – 3)(x + 5)$.

Bài giải:

a) ${x^{2}}-3x + 1$

$∆ = (- 3)^2– 4.5 < 0 \Rightarrow 5x^2- 3x + 1 > 0 , ∀x ∈\mathbb R$ (vì luôn cùng dấu với a = 5 > 0).

b) $- 2{x^2} + 3x + 5$

$f(x)=- 2{x^2} + 3x + 5=0 \Leftrightarrow \left[ \matrix{x = – 1 \hfill \cr x = {5 \over 2} \hfill \cr} \right.$

Ta có hệ số $a=-2<0$

Vậy:

$-2{x^2} + 3x + 5 < 0$ với $x \notin \left [ -1;\frac{5}{2} \right ]$

$-2{x^2} + 3x + 5 >0$ với $x \in \left ( -1;\frac{5}{2} \right )$.

c) $f(x)={x^2} +12x+36$

$\Delta ‘ = {6^2} – 1.36 = 0$

$f(x) = 0 \Leftrightarrow x = – 6$

Ta có hệ số $a=1>0$

$\Rightarrow {x^2} + 12x + 36 > 0, ∀x ≠ – 6$.

d) $f(x)=(2x – 3)(x + 5)$

$f(x) = 0 \Leftrightarrow \left[ \matrix{x = – 5 \hfill \cr x = {3 \over 2} \hfill \cr} \right.$

Ta có hệ số $a=2 > 0$.

Vậy:

$(2x – 3)(x + 5) > 0$ với $x \notin \left[-5;\frac{3}{2}\right]$

$(2x – 3)(x + 5) < 0$ với $x \in \left(-5;\frac{3}{2}\right).$

2. Giải bài 2 trang 105 sgk Đại số 10

Lập bảng xét dấu các biểu thức sau

a) $f(x) =(3{x^2} – 10x + 3)(4x – 5)$;

b) $f(x) = (3{x^2} – 4x)(2{x^2} – x – 1)$;

c) $f(x) = (4{x^2} – 1)( – 8{x^2} + x – 3)(2x + 9)$;

d) $f(x) = \frac{(3x^{2}-x)(3-x^{2})}{4x^{2}+x-3}.$

Bài giải:

a) $f(x) =(3{x^2} – 10x + 3)(4x – 5)$

$3{x^2} – 10x + 3 = 0 \Leftrightarrow \left[ \matrix{
x = {1 \over 3} \hfill \cr
x = 3 \hfill \cr} \right.$

$4x – 5 = 0 \Leftrightarrow x = {5 \over 4}$

Ta lập bảng xét dấu:

Kết luận:

$f(x) < 0$ với $x \in \left( { – \infty ;{1 \over 3}} \right) \cup \left( {{5 \over 4};3} \right)$

$f(x) > 0$ với $x \in \left( {{1 \over 3};{5 \over 4}} \right) \cup \left( {3; + \infty } \right)$

$f(x)=0$ với $x \in \left \{ \frac{1}{3}; \frac{5}{4}; 3 \right \}$

b) $f(x) = (3{x^2} – 4x)(2{x^2} – x – 1)=0$

$ \Leftrightarrow \left[ \matrix{x = 0 \hfill \cr x = {4 \over 3} \hfill \cr x = 1 \hfill \cr x = – {1 \over 2} \hfill \cr} \right.$

Ta lập bảng xét dấu:

Kết luận:

$f(x) < 0$ với $x \in \left( { – {1 \over 2}};0 \right) \cup \left( 1;{{4 \over 3}} \right)$

$f(x) > 0$ với $x \in \left( -\infty ;{-{1 \over 2}} \right) \cup (0;1) \cup \left( \frac{4}{3}; + \infty \right)$

$f(x)=0$ với $x \in \left \{ -\frac{1}{2}; 0; 1; \frac{4}{3} \right \}$

c) $f(x) = (4{x^2} – 1)( – 8{x^2} + x – 3)(2x + 9)=0$

$ \Leftrightarrow \left[ \matrix{x = {1 \over 2} \hfill \cr x = – {1 \over 2} \hfill \cr x = – {9 \over 2} \hfill \cr} \right.$

Ta lập bảng xét dấu:

Kết luận:

$f(x) < 0$ với $x \in \left( { – {9 \over 2}};-\frac{1}{2} \right) \cup \left( {{1 \over 2}}; +\infty \right)$

$f(x) > 0$ với $x \in \left( -\infty ;{-{9 \over 2}} \right) \cup \left( -\frac{1}{2}; \frac{1}{2} \right)$

$f(x)=0$ với $x \in \left \{ -\frac{9}{2}; -\frac{1}{2}; \frac{1}{2} \right \}$

d) $f(x) = \frac{(3x^{2}-x)(3-x^{2})}{4x^{2}+x-3}=0$

$ \Leftrightarrow \left[ \matrix{x = \sqrt 3 \hfill \cr x = – \sqrt 3 \hfill \cr x = {1 \over 3} \hfill \cr x = 0 \hfill \cr} \right.$

Ta lập bảng xét dấu:

Kết luận:

$f(x) < 0$ với $x \in \left( -\infty ; -\sqrt 3 \right) \cup \left( -1;0 \right) \cup \left( \frac{1}{3}; \frac{3}{4} \right) \cup (\sqrt 3; +\infty )$

$f(x) > 0$ với $x \in \left( -\sqrt 3; -1 \right) \cup \left( 0; \frac{1}{3} \right) \cup \left( \frac{3}{4}; \sqrt 3 \right)$

$f(x)=0$ với $x \in \left \{ -\sqrt 3; 0; \frac{1}{3}; \sqrt 3 \right \}$

3. Giải bài 3 trang 105 sgk Đại số 10

Giải các bất phương trình sau

a) $4{x^2} – x + 1 < 0$;

b) $ – 3{x^2} + x + 4 \ge 0$;

c) $\frac{1}{x^{2}-4}<\frac{3}{3x^{2}+x-4};$

d) $x^2- x – 6 ≤ 0$.

Bài giải:

a) $f(x) =4{x^2} – x + 1 < 0$

Ta có có hệ số $a = 4 > 0$

Biệt thức $∆ = (-1)^2- 4.4.1 < 0$.

Do đó $f(x) > 0 ,∀x ∈\mathbb R$.

Vậy bất phương trình $4{x^2} – x + 1 < 0$ vô nghiệm.

b) $ – 3{x^2} + x + 4 \ge 0$

$f(x) = – 3{x^2} + x + 4 = 0 \Leftrightarrow \left[ \matrix{x = – 1 \hfill \cr x = {4 \over 3} \hfill \cr} \right.$

Ta lại có hệ số $a=-3 <0$

Theo quy tắc trong trái dấu với a, ngoài cùng dấu với a, ta có thể xác định được tập nghiệm của bất phương trình.

Nên $ – 3{x^2} + x + 4 \ge 0 \Leftrightarrow – 1 \le x \le {4 \over 3}$

Vậy bất phương trình có tập nghiệm là $S= \left [ -1;\frac{4}{3} \right ]$

c) $\frac{1}{x^{2}-4}<\frac{3}{3x^{2}+x-4}$

$ \Leftrightarrow \frac{1}{x^{2}-4}-\frac{3}{3x^{2}+x-4}< 0$

$ \Leftrightarrow \frac{x+8}{(x^{2}-4)(3x^{2}+x-4)}< 0$

$f(x)=\frac{x+8}{(x^{2}-4)(3x^{2}+x-4)}=0$

$\Leftrightarrow \left[ \matrix{x=-8 \hfill \cr x=2 \hfill \cr x=-2 \hfill \cr x=1 \hfill \cr x=-\frac{4}{3} \hfill \cr} \right.$

Lập bảng xét dấu $f(x)$:

Tập nghiệm của bất phương trình $S = (-∞; – 8) ∪ \left(- 2; -\frac{4}{3}\right) ∪ (1; 2)$.

d) $x^2- x – 6 ≤ 0$

$x^2- x – 6 =0\Leftrightarrow \left[ \matrix{x = 3 \hfill \cr x = – 2 \hfill \cr} \right.$

Hệ số $a=1>0$

Theo quy tắc trong trái dấu với a, ngoài cùng dấu với a, ta có thể xác định được tập nghiệm của bất phương trình.

Tập nghiệm của bất phương trình là: $S =[- 2; 3]$.

4. Giải bài 4 trang 105 sgk Đại số 10

Tìm các giá trị của tham số $m$ để các phương trình sau vô nghiệm

a) $(m – 2)x^2+ 2(2m – 3)x + 5m – 6 = 0$;

b) $(3 – m)x^2- 2(m + 3)x + m + 2 = 0$.

Bài giải:

a) $(m – 2)x^2+ 2(2m – 3)x + 5m – 6 = 0$

Với $m = 2$ phương trình trở thành $2x + 4 = 0$ có $1$ nghiệm, do đó trường hợp này không thỏa mãn.

Với $m\ne 2$, phương trình vô nghiệm nếu:

$\left\{\begin{matrix} m-2\neq 0\\ \Delta ^{‘}=(2m-3)^{2}-(m-2)(5m-6)< 0 \end{matrix}\right.$

$ \Leftrightarrow \left\{\begin{matrix} m\neq 2\\ -m^{2}+4m-3< 0 \end{matrix}\right.$

$ \Leftrightarrow \left[ \matrix{m<1 \hfill \cr m>3 \hfill \cr} \right.$.

Vậy $m \in (-\infty ; 1) \cup (3; +\infty )$thì phương trình vô nghiệm.

b) $(3 – m)x^2- 2(m + 3)x + m + 2 = 0$

Với $m = 3$, phương trình trở thành: $- 6x + 5 = 0$ có nghiệm. Loại trường hợp $m = 3$.

Với $m\ne 3$, phương trình vô nghiệm khi và chỉ khi:

$\Leftrightarrow \left\{ \matrix{m \ne 3 \hfill \cr \Delta ‘ = {(m + 3)^2} – (3 – m).(m + 2) < 0 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{m \ne 3 \hfill \cr 2{m^2} + 5m + 3 < 0 \hfill \cr} \right.$

$\Leftrightarrow – {3 \over 2} < m < – 1 $

Vậy $m \in \left ( -\frac{3}{2}; -1 \right )$

Bài trước:

Giải bài 1 2 3 trang 99 sgk Đại số 10

Bài tiếp theo:

Ôn tập chương IV: Giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 trang 106 107 108 sgk Đại số 10

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 10 với giải bài 1 2 3 4 trang 105 sgk Đại số 10!

“Bài tập nào khó đã có giaibaisgk.com“