Hướng dẫn Giải bài 1 2 3 trang 128 sgk Đại số 10

Nội Dung

Hướng dẫn giải Bài §4. Phương sai và độ lệch chuẩn, Chương V. Thống kê, sách giáo khoa Đại số 10. Nội dung bài giải bài 1 2 3 trang 128 sgk Đại số 10 cơ bản bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập đại số có trong SGK để giúp các em học sinh học tốt môn toán lớp 10.

Lý thuyết

1. Phương sai

Phương sai của một bảng số liệu là số đặc trưng cho độ phân tán của các số liệu so với số trung bình của nó. Phương sai của bảng thống kê dấu hiệu $x$, kí hiệu là $S_x^2$. Công thức tính phương sai như sau:

a) Đối với bảng phân bố rời rạc

$x_i$	$x_1$	$x_2$	…	$x_k$
Tần số	$n_1$	$n_2$	…	$n_k$

$ n_1+ n_2 +…+ n_n= n$

$S_{x}^{2}=\frac{1}{n}[n_{1}(x_{1}-\overline{x})^{2}+n_{2}(x_{2}-\overline{x})^{2}+…+n_{k}(x_{k}-\overline{x})^{2}]$

$=\frac{1}{n}(n_{1}x_{1}^{2}+n_{2}x_{2}^{2}+…+n_{k}x_{1}^{2})-(\overline{x})^{2}.$

trong đó $\overline{x}$ là số trung bình của bảng số liệu.

b) Đối với phân bố tần số ghép lớp

$S_{x}^{2}=\frac{1}{n}[n_{1}(C_{1}-\overline{x})^{2}+n_{2}(C_{2}-\overline{x})^{2}+…+n_{k}(C_{k}-\overline{x})^{2}+].$

trong đó $C_i(i = 1, 2,…, k)$ là giá trị trung tâm của lớp thứ $i$.

$\overline{x}$ là số trung bình của bảng.

2. Độ lệch chuẩn

Căn bậc hai của phương sai một bảng số liệu gọi là độ lệch chuẩn của bảng đó. Độ lệch chuẩn của dấu hiệu $x$, kí hiêu là $S_x$.

$S_x= \sqrt{S_{x}^{2}}.$

Ghi chú: các công thức về phương sai có thể viết gọn nhờ kí hiệu $\sum$ như sau:

$S_{x}^{2}=\frac{1}{n}\sum_{i=1}^{k}n_{i}(x_{i}-\overline{x})^{2}= \sum_{i=1}^{n}f_{i}(x_{i}-\overline{x})^{2}$

$=\frac{1}{n}\sum_{i=1}^{k}n_{i}x_{i}^{2}-(\overline{x})^{2}=\sum_{i=1}^{k}f_{i}x_{i}^{2}-(\overline{x})^{2}.$

Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong phần hoạt động của học sinh sgk Đại số 10.

Câu hỏi

1. Trả lời câu hỏi 1 trang 126 sgk Đại số 10

Tính phương sai của bảng $6$ (ở §2).

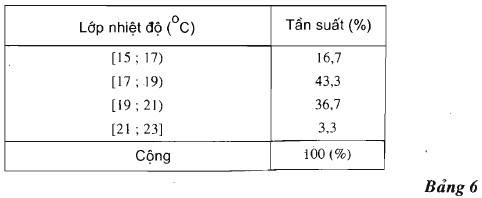
Trả lời:

Ta có:

${s^2} = {{16,7} \over {100}}{(16 – 18,5)^2} $+$ {{43,3} \over {100}}{(18 – 18,5)^2}$ + ${{36,7} \over {100}}{(20 – 18,5)^2} $+$ {{3,3} \over {100}}{(22 – 18,5)^2}$ $\approx 2,382$

Vậy phương sai $\approx 2,382$

2. Trả lời câu hỏi 2 trang 126 sgk Đại số 10

Hãy tính độ lệch chuẩn của bảng 6 (ở §2).

Trả lời:

Ta có:

Độ lệch chuẩn:

$S = \sqrt{s^2} = \sqrt{2,382} \approx 1,54$

Dưới đây là phần Hướng dẫn giải bài 1 2 3 trang 128 sgk Đại số 10 cơ bản. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập đại số 10 kèm bài giải chi tiết bài 1 2 3 trang 128 sgk Đại số 10 cơ bản của Bài §4. Phương sai và độ lệch chuẩn trong Chương V. Thống kê cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 1 trang 128 sgk Đại số 10

Tính phương sai và độ lệch chuẩn của bảng phân bố tần số đã được lập ở bài tập $1$ và của bảng phân bố tần số ghép lớp cho ở bài tập $2$ của §1.

Bài giải:

♦ Bài tập $1$ của §1:

Bảng phân bố tần số viết lại là:

$x_i$	$1150$	$1160$	$1170$	$1180$	$1190$
Tần số	$3$	$6$	$12$	$6$	$3$

Số trung bình về tuổi thọ của bóng đèn trong bảng phân bố trên là:

$\overline{x}=\frac{3.1150 + 6.1160 + 12.1170 + 6.1180 + 3.1190}{30}=\frac{35100}{30}= 1170$.

Phương sai:

$S_{x}^{2}=\frac{3(1150-1170)^2+6(1160-1170)^{2}+12(1170-1170)^{2}+6(1180-1170)^{2}+3(1190-1170)^{2}}{30}= 120$

Độ lệch chuẩn: $S_x= \sqrt{S_{x}^{2}}=\sqrt{120} ≈ 11$(giờ)

♦ Bài tập $2$ của §1:

Số trung bình về chiều dài lá cây dương xỉ là:

$\overline{x}=\frac{8.15 + 18.25 + 24.35 + 10.45}{60}=\frac{1860}{60}= 31 (cm)$.

Phương sai:

$S_{x}^{2}=\frac{8(15-31)^{2}+18(25-31)^{2}+24(35-31)^{2}+10(45-31)^{2}}{60}= 84 $

Độ lệch chuẩn: $S_x = \sqrt{S_x^2}≈ 9,2$.

2. Giải bài 2 trang 128 sgk Đại số 10

Hai lớp $10C, 10D$ của một trường Trung học phổ thông đồng thời làm bài thi môn Ngữ văn theo cùng một đề thi. Kết quả thi được thình bày ở hai bảng phân bố tần số sau đây:

a) Tính các số trung bình cộng, phương sai, độ lệch chuẩn của các bảng phân bố tần số đã cho.

b) Xét xem kết quả làm bài thi của môn Ngữ văn ở lớp nào là đồng đều hơn?

Bài giải:

a) Số trung bình điểm thi Ngữ văn của lớp $10C$ là:

$\overline{x}=\frac{3.5 + 7. 6 + 12.7 + 14. 8 + 3.9 + 1.10}{40}= 7,25$

$\overline{x^2}=\frac{3.5^2 + 7. 6^2 + 12.7^2 + 14. 8^2 + 3.9^2 + 1.10^2}{40}= 53,85$

Phương sai bảng điểm thi Văn của lớp $10C$ là:

$S_{x}^{2}=\overline{x^2}-\overline{x}^2=53,86-(7,25)^2= 1,2875$

Độ lệch chuẩn bảng điểm thi Văn của lớp $10C$ là:

$S_x = \sqrt{S_x^2}≈ 1,1347$

Số trung bình điểm thi Ngữ văn của lớp $10D$ là:

$\overline{y}=\frac{8.6+18.7+10.8+4.9}{40}= 7,25$

$\overline{y^2}=\frac{8.6^2+18.7^2+10.8^2+4.9^2}{40}= 53,35$

Phương sai bảng điểm thi Văn của lớp $10D$ là:

$S_{y}^{2}=\overline{y^2}-\overline{y}^2=53,35-(7,25)^2= 0,7875$

Độ lệch chuẩn bảng điểm thi Văn của lớp $10D$ là:

$S_y = \sqrt{S_y^2}≈ 0,8874$.

b) Phương sai của bảng điểm thi lớp $10D$ nhỏ hơn phương sai của bảng điểm thi lớp $10C$. Vậy kết quả làm bài thi Văn ở lớp $10D$ đồng đều hơn.

3. Giải bài 3 trang 128 sgk Đại số 10

Cho hai bảng phân bố tần số ghép lớp

a) Tính các số trung bình cộng của các bảng phân bố tần số ghép lớp đã cho.

b) Tính phương sai của các bảng phân bố tần số ghép lớp đã cho.

c) Xét xem nhóm cá nào có khối lượng đồng đều hơn?

Bài giải:

a), b) ♦ Đối với nhóm cá thứ nhất:

Số trung bình cộng của nhóm cá thứ nhất:

$\overline{x}=\frac{4.0,7 + 6.0,9 + 6. 1,1 + 4.1,3}{20}= 1$

Phương sai:

$S_{x}^{2}=\frac{4.0,7^2 + 6.0,9^2 + 6. 1,1^2 + 4.1,3^2}{20} = 0,042$

Độ lệch chuẩn:

$S_x = \sqrt{S_x^2}≈ 0,2$

♦ Đối với nhóm cá thứ hai:

Số trung bình cộng của nhóm cá thứ hai:

$\overline{y}=\frac{3.0,6 + 4.0,8 + 6.1 + 4.1,2 + 3.1,4}{20} = 1$

Phương sai:

$S_{x}^{2}=\frac{3.0,6^2 + 4.0,8^2 + 6.1^2 + 4.1,2^2 + 3.1,4^2}{20}= 0,064$

Độ lệch chuẩn:

$S_x = \sqrt{S_x^2} = \sqrt{0,064} ≈ 0,25$.

c) Ta thấy $\overline{x}=\overline{y}= 1$

Trọng lượng trung bình hai nhóm cá bằng nhau. Nhưng $S_{x}^{2} < S_{y}^{2}$nên mức độ phân tán các giá trị so với giá trị trung bình của nhóm cá thứ hai lớn hơn. Tức là khối lượng nhóm cá thứ nhất đồng đều hơn nhóm cá thứ hai.

Bài trước:

Giải bài 1 2 3 4 5 trang 122 123 sgk Đại số 10

Bài tiếp theo:

Ôn tập chương V: Giải bài 1 2 3 4 5 6 7 9 10 11 trang 128 129 130 131 sgk Đại số 10

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 10 với giải bài 1 2 3 trang 128 sgk Đại số 10!

“Bài tập nào khó đã có giaibaisgk.com“

\(x_i\)	\(x_1\)	\(x_2\)	…	\(x_k\)
Tần số	\(n_1\)	\(n_2\)	…	\(n_k\)