Nội Dung
Hướng dẫn giải Bài Ôn tập Chương V. Thống kê, sách giáo khoa Đại số 10. Nội dung bài giải bài 1 2 3 4 5 6 7 9 10 11 trang 128 129 130 131 sgk Đại số 10 cơ bản bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập đại số có trong SGK để giúp các em học sinh học tốt môn toán lớp 10.
Lý thuyết
1. Bảng phân bố tần số và tần suất
2. Biểu đồ
3. Số trung bình cộng. Số trung vị. Mốt
4. Phương sai và độ lệch chuẩn
Dưới đây là phần Hướng dẫn giải bài 1 2 3 4 5 6 7 9 10 11 trang 128 129 130 131 sgk Đại số 10 cơ bản. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập đại số 10 kèm bài giải chi tiết bài 1 2 3 4 5 6 7 9 10 11 trang 128 129 130 131 sgk Đại số 10 cơ bản của Bài Ôn tập Chương V. Thống kê cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
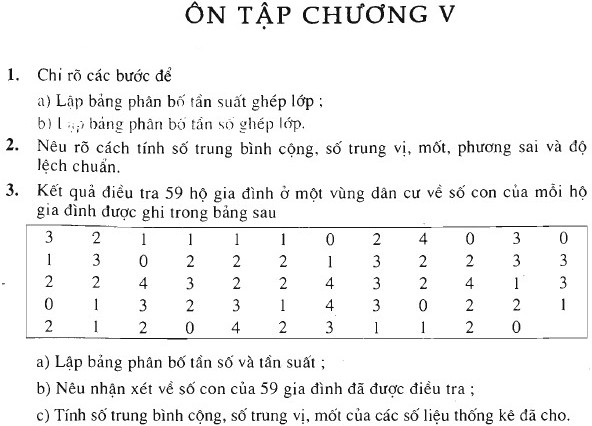
1. Giải bài 1 trang 128 sgk Đại số 10
Chỉ rõ các bước để:
a) Lập bảng phân bố tần suất ghép lớp.
b) Lập bảng phân bố tần số ghép lớp.
Trả lời:
a) Lập bảng phân bố tần suất ghép lớp
– Bước 1. Chia bảng số liệu thống kế rời rạc thành các lớp
– Bước 2. Ghi các số liệu thống kế của mỗi lớp ghép vào cột “tần số”
– Bước 3. Tính tỉ số (phần trăm) của tần số mỗi lớp chia cho tổng các số liệu thống kế, ghi kết quả vào cột “tần suất”.
b) Lập bảng phân bố tần số ghép lớp
– Bước 1. Chia bảng số liệu thống kế rời rạc thành các lớp
– Bước 2. Ghi các số liệu thống kế của mỗi lớp ghép vào cột “tần số”
2. Giải bài 2 trang 129 sgk Đại số 10
Nêu rõ cách tính của số trung bình cộng, số trung vị, mốt, phương sai và độ lệch chuẩn.
Trả lời:
♦ Số trung bình cộng:
– Bảng phân bố rời rạc:
\(\bar{x}={1 \over n}({n_1}{x_1} + {n_2}{x_2} + … + {n_k}{x_k}) = {f_1}{x_1} + {f_2}{x_2} + … + {f_k}{x_k}\)
– Bảng phân bố ghép lớp:
\(\bar{x} = {1 \over n}({n_1}{c_1} + {n_2}{c_2} + … + {n_k}{x_k}) = {f_1}{c_1} + {f_2}{c_2} + … + {f_k}{c_k}\)
Trong tất cả các trường hợp:
\(n\) là số các số liệu thống kê.
\(n_i\) là tần số của giá trị \(x_i\).
\(c_i\) là giá trị trung tâm của lớp ghép.
\(f_i\) là tần suất của giá trị \(x_i,\) của giá trị trung tâm \(c_i\).
♦ Số trung vị:
– Bước 1. Sắp thứ tự các số liệu thống kế thành dãy không giảm
– Bước 2. Số đứng giữa của dãy này là số trung vị \(M_e\)
(Nếu trong dãy này có hai số đứng giữa thì số trung vị là trung bình cộng của hai số đứng giữa này).
♦ Mốt: Đó là giá trị có tần số lớn nhất.
♦ Phương sai:
– Bước 1. Tìm số trung bình cộng \(\bar{x}\)
– Bước 2. Bình phương các độ lệch của mỗi số liệu \({\left( {{x_i} – \overline x } \right)^2}\)
– Bước 3. Tìm trung bình cộng của \({\left( {{x_i} – \overline x } \right)^2}\)
⇒ Kết quả là \(S^2\) (phương sai)
♦ Độ lệch chuẩn:
– Bước 1. Tính phương sai : \(S^2\)
– Bước 2. Căn bậc hai của \(S^2\). Đó là độ lệch chuẩn
3. Giải bài 3 trang 129 sgk Đại số 10
Kết quả điều tra \(59\) hộ gia đình ở một vùng dân cư về số con của mỗi hộ gia đình là:

a) Lập bảng phân bố tần số và tần suất
b) Nêu nhận xét về số con của \(59\) gia đình đã được điều tra
c) Tính số trung bình cộng, số trung vị, mốt của các số liệu thống kế đã cho.
Bài giải:
a) Bảng phân bố tần số và tần suất
| Số con trong một hộ | Tần số | Tần suất (%) |
| $0$ | $8$ | $13,56$ |
| $1$ | $13$ | $22,03$ |
| $2$ | $19$ | $32,21$ |
| $3$ | $13$ | $22,03$ |
| $4$ | $6$ | $10,17$ |
| Cộng | $59$ | $100$ |
b) Nhận xét:
– Số hộ có $1$ con, $2$ con và $3$ con là đa số.
– Số hộ có \(2\) con chiếm tỉ lệ cao nhất \(32,21\%\)
c) Số trung bình:
\(\bar{x}= {1 \over {59}}(15.1+22.2+16.3+6.4) ≈ 2,22\)
Mốt: \(M_0 = 2\)
Số trung vị: \(M_e= 2\)
4. Giải bài 4 trang 129 sgk Đại số 10
Cho các số liệu thống kê được ghi trong 2 bảng dưới đây:

a) Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 1 với các lớp là
$[630; 635) ; [635;640) $; $[640; 645) ; [645; 650)$ ; $[650; 655]$
b) Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 1 với các lớp là:
$[638;642) ; [642; 646)$ ; $[646;650) ; [650; 654]$
c) Mô tả bảng phân bố tần suất ghép lớp đã được lập ở câu a) bằng cách vẽ biểu đồ tần suất hình cột và đường gấp khúc tần suất.
d) Mô tả bảng phân bố tần suất ghép lớp đã được lập ở câu b) bằng cách vẽ biểu đồ tần số hình cột và đường gấp khúc tần số.
e) Tính số trung bình cộng, phương sai và độ lệch chuẩn của các bảng phân bố tần số và tần suất ghép lớp đã lập được.
Từ đó, xét xem nhóm cá nào có khối lượng đồng đều hơn.
Bài giải:
a) Bảng phân bố tần số và tần suất ghép lớp của nhóm các thứ nhất.
| Lớp khối lượng (gam) | Tần số | Tần suất |
| \([630;635)\) | $1$ | $4,2$ |
| \([635;640)\) | $2$ | $8,3$ |
| \([640;645)\) | $3$ | $12,5$ |
| \([645;650)\) | $6$ | $25,0$ |
| \([650;655]\) | $12$ | $50,0$ |
| Cộng | $24$ | $100$ |
b) Bảng phân bố tần số và tần suất ghép lớp của nhóm cá thứ hai
| Lớp khối lượng (gam) | Tần số | Tần suất (%) |
| \([638, 642)\) | $5$ | $19$ |
| \([642, 646)\) | $9$ | $33$ |
| \([646, 650\) | $1$ | $4$ |
| \([650, 645]\) | $12$ | $44$ |
| Cộng | $27$ | $100$ |
c) Biểu đồ hình cột và đường gấp khúc tần suất bảng phân bố tần suất ghép lớp trong câu a)
Biểu đồ hình cột:

Đường gấp khúc tần suất:

d) Biểu đồ hình cột và đường gấp khúc tần suất của bảng phân bố tần số ghép lớp trong câu b)
Biểu đồ hình cột:

Đường gấp khúc tần suất:

e) Số trung bình, phương sai và độ lệch chuẩn của bảng phân bố tần số và tần suất ghép lớp thứ nhất:
\(\bar{x}={{1.632,5 + 2.637,5 + 3.642,5 + 6.647,5 + 12.652,5} \over {24}}≈ 647,92(gam)\)
\(S_x^2 = {{1.(632,5-648)^2 + 2.(637,5-648)^2 + 3.(642,5-648)^2 + 6.(647,5-648)^2.6 + 12.(652.5-648)^2} \over {24}}= 33,16\)
\(⇒S_x≈ 5,76\)
Số trung bình, phương sai và độ lệch chuẩn của bảng phân bố tần số và tần suất ghép lớp thứ hai:
\(\bar{y}=\frac{5.640+9.644+1.648+12.652}{27}\approx 647\)
\(S_y^2=\frac{5.(640-647)^2+9.(644-647)^2+1.(648-647)^2+12.(652-647)^2}{27}\approx 23,22\)
\(⇒ S_y= 4,82\)
Nhận xét: Độ lệch chuẩn của nhóm cá thứ hai nhỏ hơn nhóm cá thứ nhất nên khối lượng các con cá nhóm thứ hai đồng đều hơn nhóm thứ nhất.
5. Giải bài 5 trang 130 sgk Đại số 10
Cho dãy số liệu thống kế được ghi trong bảng sau:
Mức lương hàng năm của các cán bộ và nhân viên trong một công ty (đơn vị nghìn đồng)

Tìm mức lương trung bình của các cán bộ và nhân viên công ty, số trung bình của dãy số liệu.
Nêu ý nghĩa của số trung vị.
Bài giải:
Mức lương bình quân của nhân viên công ty là số trung bình của bảng lương.
\(\bar{x}=\frac{20060 + 20110 + 20350.2 + 20910 + 20960 + 21130 + 21360 + 21410.2 + 76000 + 125000}{12} = 34087,5\) nghìn đồng
Sắp xếp theo thứ tự không giảm bảng lương ta được:
| $20060$ | $20110$ | $20350$ | $20350$ | $20910$ | $20960$ |
| $21130$ | $21360$ | $21410$ | $21410$ | $76000$ | $125000$ |
Số trung vị:
\(M_e= {{20960 + 21130} \over 2} = 21045\) (nghìn đồng)
Số trung vị phân chia dãy số liệu sắp thứ tự thành hai phần bằng nhau, nghĩa là số người có lương dưới $21045$ bằng số người có lương trên $21045$ (nghìn đồng)
6. Giải bài 6 trang 130 sgk Đại số 10
Người ta tiến hành thăm dò ý kiến khách hàng về các mẫu $1, 2, 3, 4, 5$ của một loại sản phẩm mới được sản xuất ở một nhà máy. Dưới đây là bảng phân bố tần số theo số phiếu tín nhiệm dành cho các mẫu kể trên.

a) Tìm mốt của bảng phân bố tần số đã cho
b) Trong sản xuất, nhà máy nên ưu tiên mẫu nào?
Bài giải:
a) Giá trị $1$ (Mẫu số $1$) là mốt của bảng phân bố vì có tần số lớn nhất là $2100.$
b) Nhà máy ưu tiên sản xuất mẫu số $1$ vì nhu cầu tiêu thụ, lượng khách hàng lớn hơn.
Bài tập trắc nghiệm
Chọn phương án đúng trong các bài tập sau
7. Giải bài 7 trang 130 sgk Đại số 10
Cho bảng phân bố tần số.

Bài giải:
Số tiền 3 triệu đồng có tần số lớn nhất là 15
Vậy chọn đáp án (C)
8. Giải bài 8 trang 131 sgk Đại số 10
Cho bảng phân bố tần số:

Bài giải:
Sắp xếp theo thứ tự không giảm số liệu thứ \(85\) là số trung vị.
Vậy chọn đáp án (B)
9. Giải bài 9 trang 131 sgk Đại số 10
Cho dãy số liệu thống kê
\(21; 23; 24; 25; 22; 20\)
Số trung bình cộng của các số liệu thống kê đã cho bằng:
| (A) \(23,5\) | (B) \(22\) |
| (C) \(22,5\) | (D) \(14\) |
Bài giải:
Số trung bình:
\(\bar{x}=\frac{21 + 23 + 24 + 25 + 22 + 20}{6} = 22,5\)
Vậy chọn đáp án (C)
10. Giải bài 10 trang 131 sgk Đại số 10
Cho bảng thống kế:
\(1, 2, 3, 4, 5, 6, 7\)
Phương sai của các số liệu thống kê đã cho là:
| (A) \(1\) | (B) \(2\) |
| (C) \(3\) | (D) \(4\) |
Bài giải:
Số trung bình: \({1 \over 7}(1 + 2 + 3 + 4 + 5 + 6 + 7) = 4\)
Phương sai:
\(S_x^2=\frac{(1-4)^2+(2-4)^2+(3-4)^2+(4-4)^2+(5-4)^2+(6-4)^2+(7-4)^2}{7}= 4\)
Vậy chọn đáp án (D)
11. Giải bài 11 trang 131 sgk Đại số 10
Ba nhóm học sinh gồm 10 người, 15 người, 25 người. Khối lượng trung bình của mỗi nhóm lần lượt là: 50kg, 38kg, 40kg
Khối lượng trung bình của ba nhóm học sinh là:
| (A) \(41,4 kg\) | (B) \(42,4 kg\) |
| (C) \(26 kg\) | (D) \(37 kg\) |
Bài giải:
Khối lượng trung bình của cả 3 nhóm học sinh là:
\(\bar{x}=\frac{50.10+38.15+40.25}{10+15+25} = 41,4\) (kg)
Vậy chọn đáp án (A)
Bài trước:
Xem thêm:
- Các bài toán 10 khác
- Để học tốt môn Vật lí lớp 10
- Để học tốt môn Sinh học lớp 10
- Để học tốt môn Ngữ văn lớp 10
- Để học tốt môn Lịch sử lớp 10
- Để học tốt môn Địa lí lớp 10
- Để học tốt môn Tiếng Anh lớp 10
- Để học tốt môn Tiếng Anh lớp 10 thí điểm
- Để học tốt môn Tin học lớp 10
- Để học tốt môn GDCD lớp 10
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 10 với giải bài 1 2 3 4 5 6 7 9 10 11 trang 128 129 130 131 sgk Đại số 10!
“Bài tập nào khó đã có giaibaisgk.com“
