Toán lớp 10

Ôn tập cuối năm: Giải bài 1 2 3 4 5 6 7 8 9 trang 98 99 sgk Hình học 10

Hướng dẫn giải bài Ôn tập cuối năm Hình học 10. Nội dung bài giải bài 1 2 3 4 5 6 7 8 9 trang 98 99 sgk Hình học 10 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập hình học có trong SGK để giúp các em học sinh học tốt môn toán lớp 10.

Lý thuyết

1. Chương I. Vectơ

2. Chương II. Tích vô hướng của hai vectơ và ứng dụng

3. Chương III. Phương pháp tọa độ trong mặt phẳng

Dưới đây là phần Hướng dẫn giải bài 1 2 3 4 5 6 7 8 9 trang 98 99 sgk Hình học 10. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập ôn tập cuối năm

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập hình học 10 kèm bài giải chi tiết bài 1 2 3 4 5 6 7 8 9 trang 98 99 sgk Hình học 10 của Bài Ôn tập cuối năm Hình học 10 cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 6 7 8 9 trang 98 99 sgk Hình học 10
Giải bài 1 2 3 4 5 6 7 8 9 trang 98 99 sgk Hình học 10

1. Giải bài 1 trang 98 sgk Hình học 10

Cho hai vectơ \(a\) và \(b\) sao cho \(|\overrightarrow a | = 3;|\overrightarrow b | = 5;(\overrightarrow a ,\overrightarrow b ) = {120^0}\) . Với giá trị nào của m thì hai vectơ \(\overrightarrow a + m\overrightarrow b \) và \(\overrightarrow a – m\overrightarrow b \) vuông góc với nhau?

Bài giải:

Hai vectơ \(\overrightarrow{a}+m\overrightarrow{b}\) và \(\overrightarrow{a}-m\overrightarrow{b}\) vuông góc với nhau thì:
\(\begin{aligned} & \left( \overrightarrow{a}+m\overrightarrow{b} \right) \left( \overrightarrow{a}-m\overrightarrow{b} \right)=0 \\ & \Leftrightarrow {{\left( \overrightarrow{a} \right)}^{2}}-m\overrightarrow{a}\overrightarrow{b}+m\overrightarrow{a}\overrightarrow{b}-{{m}^{2}}{{\left( \overrightarrow{b} \right)}^{2}}=0 \\ & \Leftrightarrow {{\left| \overrightarrow{a} \right|}^{2}}-m\left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|\cos \left( \overrightarrow{a},\overrightarrow{b} \right)+m\left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|\cos \left( \overrightarrow{a},\overrightarrow{b} \right)-{{m}^{2}}{{\left| \overrightarrow{b} \right|}^{2}}=0 \\ & \Leftrightarrow 9-25{{m}^{2}}=0 \\ & \Leftrightarrow m=\pm \dfrac{3}{5} \\ \end{aligned}\)

Vậy với \(m=\pm \dfrac{3}{5}\) thì hai vectơ \(\overrightarrow{a}+m\overrightarrow{b}\) và \(\overrightarrow{a}-m\overrightarrow{b}\) vuông góc với nhau.

2. Giải bài 2 trang 98 sgk Hình học 10

Cho tam giác \(ABC\) có hai điểm \(M,N\) sao cho

\(\left\{ \matrix{
\overrightarrow {AM} = \alpha \overrightarrow {AB} \hfill \cr
\overrightarrow {AN} = \beta \overrightarrow {AC} \hfill \cr} \right.\)

a) Hãy vẽ \(M, N\) khi \(\alpha = {2 \over 3};\beta = – {2 \over 3}\)

b) Hãy tìm mối liên hệ giữa \(α, β\) để \(MN//BC\)

Bài giải:

a) Ta có:

\(\eqalign{
& \overrightarrow {AM} = {2 \over 3}\overrightarrow {AB} \Leftrightarrow \left\{ \matrix{
\overrightarrow {AM} \uparrow \uparrow \overrightarrow {AB} \hfill \cr
AM = {2 \over 3}AB \hfill \cr} \right. \cr
& \overrightarrow {AN} = – {2 \over 3}\overrightarrow {AC} \Leftrightarrow \left\{ \matrix{
\overrightarrow {AN} \uparrow \downarrow \overrightarrow {AC} \hfill \cr
AN = {2 \over 3}AC \hfill \cr} \right. \cr} \)

Vậy \(M\) thuộc đoạn \(AB\) sao cho \(AM = {2 \over 3}AB \) và \(N\) thuộc tia đối của tia \(AC\) sao cho \(AN = {2 \over 3}AC .\)

b) Ta có:

\(\eqalign{
& \overrightarrow {AM} = \alpha \overrightarrow {AB} \cr
& \overrightarrow {AN} = \beta \overrightarrow {AC} \cr
& \Rightarrow \overrightarrow {AM} – \overrightarrow {AN} = \alpha \overrightarrow {AB} – \beta \overrightarrow {AC} \cr
& \Rightarrow \overrightarrow {MN} = \alpha \overrightarrow {AB} – \beta \overrightarrow {AC} \cr
& \Rightarrow \overrightarrow {MN} = \alpha (\overrightarrow {AB} – {\beta \over \alpha }\overrightarrow {AC} ),\alpha \ne 0 \cr} \)

Ta cũng có: \(\overrightarrow {BC} = – (\overrightarrow {AB} – \overrightarrow {AC} )\)

Do đó, để \(MN // BC\) thì

\(\begin{array}{l}
\overrightarrow {MN} = k\overrightarrow {BC} \\ \Leftrightarrow \beta \overrightarrow {AC} – \alpha \overrightarrow {AB} = k\overrightarrow {AC} – k\overrightarrow {AB} .\\
\Rightarrow \beta = \alpha = k.
\end{array}\)

Vậy \(MN//BC \Leftrightarrow \beta = \alpha .\)

3. Giải bài 3 trang 99 sgk Hình học 10

Cho tam giác đều \(ABC\) cạnh \(a\)

a) Cho \(M\) là một điểm trên đường tròn ngoại tiếp tam giác \(ABC\). Tính \(MA^2+ MB^2+ MC^2\) theo \(a\)

b) Cho đường thẳng \(a\) tùy ý, tìm điểm \(N\) trên đường thẳng \(d\) sao cho \(NA^2+ NB^2 + NC^2\) nhỏ nhất.

Bài giải:

a) Ta có:

\(\eqalign{
& \overrightarrow {MA} = \overrightarrow {OA} – \overrightarrow {OM} \cr
& {\overrightarrow {MA} ^2} = {(\overrightarrow {OA} – \overrightarrow {OM} )^2}\cr&\;\;\;\;\;\;\;\;\;\, = {\overrightarrow {OA} ^2} + {\overrightarrow {OM} ^2} – 2\overrightarrow {OA} .\overrightarrow {OM} \cr
& \Rightarrow {\overrightarrow {MA} ^2} = 2{R^2} – 2\overrightarrow {OA} .\overrightarrow {OM} (1) \cr} \)

Tương tự ta có:

\(\eqalign{
& M{B^2} = {\overrightarrow {MB} ^2} = 2{R^2} – 2\overrightarrow {OB} .\overrightarrow {OM} (2) \cr
& M{C^2} = {\overrightarrow {MC} ^2} = 2{R^2} – 2\overrightarrow {OC.} \overrightarrow {OM} (3) \cr} \)

Từ (1), (2) và (3) suy ra:

\(M{A^2} + M{B^2} + M{C^2}\)\( = 6{R^2} – 2\overrightarrow {OM} (\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} )\)

Tam giác \(ABC\) là tam giác đều nội tiếp đường tròn tâm \(O\) nên \(O\) cũng là trọng tâm của tam giác \(ABC\), cho ta \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0\)

Vậy \(M{A^2} + M{B^2} + M{C^2} = 6{R^2} \)

Vì đường tròn ngoại tiếp tam giác đều cạnh \(a\) nên ta có:

\(a = R\sqrt3 ⇒ 6R^2= 2(R\sqrt3)^2\)

Vậy \(M{A^2} + M{B^2} + M{C^2} = 2a^2\)

b) Gọi \(G\) là trọng tâm của tam giác ta có:

\(\eqalign{
& \overrightarrow {NA} = \overrightarrow {NG} + \overrightarrow {GA} \cr
& \Rightarrow {\overrightarrow {NA} ^2} = {\overrightarrow {GA} ^2} + 2\overrightarrow {NG} .\overrightarrow {GA} + {\overrightarrow {GA} ^2} \cr} \)

Tương tự ta có:

\(\eqalign{
& {\overrightarrow {NB} ^2} = {\overrightarrow {NG} ^2} + 2\overrightarrow {NG} .\overrightarrow {GB} + {\overrightarrow {GB} ^2} \cr
& {\overrightarrow {NC} ^2} = {\overrightarrow {NG} ^2} + 2\overrightarrow {NG} .\overrightarrow {GC} + {\overrightarrow {GC} ^2} \cr} \)

\(\Rightarrow N{A^2} + N{B^2} + N{C^2} \)\(= 3N{G^2} + 2\overrightarrow {NG} (\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} )\)\( + G{A^2} + G{B^2} + G{C^2}\)

Vì \(G\) là trọng tâm của tam giác

\(⇒\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)

\(\eqalign{
& {\overrightarrow {GA} ^2} + {\overrightarrow {GB} ^2} + {\overrightarrow {GC} ^2} = 3G{A^2} \cr&= 3.{({2 \over 3}.{{a\sqrt 3 } \over 2})^2} = {a^2} \cr
& \Rightarrow N{A^2} + N{B^2} + N{C^2} = {a^2} + 3N{G^2} \cr} \)

\(a^2\) là số không đổi nên tổng \(N{A^2} + N{B^2} + N{C^2}\) nhỏ nhất khi \(NG\) đạt giá trị nhỏ nhất. Vì \(NG\) là khoảng cách từ \(G\) đến điểm \(N\) thuộc đường thẳng \(d\) nên \(NG\) nhỏ nhất khi \(NG⊥d\) hay \(N\) là hình chiếu của trọng tâm \(G\) trên đường thẳng \(d\).

4. Giải bài 4 trang 99 sgk Hình học 10

Cho tam giác đều \(ABC\) có cạnh bằng \(6cm\). Một điểm \(M\) nằm trên cạnh \(BC\) sao cho \(BM = 2cm\)

a) Tính độ dài của đoạn thẳng \(AM\) và tính cosin của góc \(BAM\)

b) Tính bán kính đường tròn ngoại tiếp tam giác \(ABM.\)

c) Tính độ dài đường trung tuyến vẽ từ \(C\) của tam giác \(ACM.\)

d) Tính diện tích tam giác \(ABM.\)

Bài giải:

a) Ta có:

\( A{M^2} = B{A^2} + B{M^2}\)\( – 2BA.BM.\cos\widehat {ABM}\)

\(\eqalign{
& \Rightarrow A{M^2} = 36 + 4 – 2.6.2.{1 \over 2} \cr
& \Rightarrow A{M^2} = 28 \Rightarrow AM = 2\sqrt 7 (cm) \cr} \)

Ta cũng có:

\(\eqalign{
& \cos \widehat {BAM }= {{A{B^2} + A{M^2} – B{M^2}} \over {2AB.AM}} \cr
& \Rightarrow \cos\widehat { BAM }= {{5\sqrt 7 } \over {14}} \cr} \)

b) Trong tam giác \(ABM\), theo định lí Sin ta có:

\(\eqalign{
& {{AM} \over {\sin \widehat {ABM}}} = 2R \Leftrightarrow R = {{AM} \over {2\sin \widehat {ABM}}} \cr
& R = {{2\sqrt 7 } \over {2\sin {{60}^0}}} = {{2\sqrt {21} } \over 3}(cm) \cr} \)

c) Áp dụng công thức đường trung tuyến ta có:

\(\eqalign{
& C{P^2} = {{C{A^2} + C{M^2}} \over 2} – {{A{M^2}} \over 4} \cr
& \Rightarrow C{P^2} = {{36 + 16} \over 2} – {{28} \over 4} \cr
& \Rightarrow C{P^2} = 19 \Rightarrow CP = \sqrt {19} \cr}\)

d) Diện tích tam giác \(ABM\) là:

\(S = {1 \over 2}BA.BM\sin \widehat {ABM} \)\(= {1 \over 2}6.2\sin {60^0} = 3\sqrt 3 (c{m^2})\)

5. Giải bài 5 trang 99 sgk Hình học 10

Chứng minh rẳng trong mọi tam giác ABC ta đều có:

a) \(a = b \cos C + c \cos B\)

b) \(\sin A = \sin B.\cos C + \sin C.\cos B\)

c) \(h_a= 2R.\sin B\sin C.\)

Bài giải:

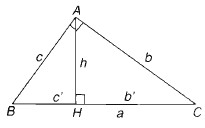
a) Trong tam giác \(ABC\), theo định lí cosin ta có:

\(\left\{ \matrix{
\cos C = {{{a^2} + {b^2} – {c^2}} \over {2ab}} \hfill \cr
\cos B = {{{a^2} + {c^2} – {b^2}} \over {2ac}} \hfill \cr} \right.\)

Ta có:

\(\eqalign{
& b\cos C + c\cos B \cr&= b({{{a^2} + {b^2} – {c^2}} \over {2ab}}) + c({{{a^2} + {c^2} – {b^2}} \over {2ac}}) \cr
& = {{2{a^2} + {b^2} – {c^2} + {c^2} – {b^2}} \over {2a}} \cr} \)

Vậy \(a = b \cos C + c \cos B\)

b) Trong tam giác \(ABC\) , theo định lí sin:

\(\eqalign{
& {a \over {\sin A}} = {b \over {{\mathop{\rm sinB}\nolimits} }} = {c \over {\sin C}} = 2R \cr
& \Rightarrow \sin A = {a \over {2R}},\cr&\;\;\;\;\;\sin B = {b \over {2R}},\cr&\;\;\;\;\;\sin C = {c \over {2R}} \cr} \)

Ta có:

\(\eqalign{
& \sin B\cos C + \sin C\cos B \cr
& = {b \over {2R}}.{{{a^2} + {b^2} – {c^2}} \over {2ab}}\cr&\;\;\;\; + {c \over {2R}}.{{{a^2} + {c^2} – {b^2}} \over {2ac}} \cr
& = {a \over {2R}} = \sin A \cr} \)

c) Ta lại có: \(a.{h_a} = 2S \Rightarrow {h_a} = {{2S} \over a}\)

mà \(S = {{abc} \over {4R}} \Rightarrow {h_a} = {{2bc} \over {4R}} = {{bc} \over {2R}}(2)\)

Thế \(b = 2RsinB, c = 2Rsin C\) vào (2) ta được:

\({h_a} = {{2R{\mathop{\rm sinB}\nolimits} .2RsinC} \over {2R}}\)\( \Rightarrow {h_a} = 2R\sin B\sin C\)

6. Giải bài 6 trang 99 sgk Hình học 10

Cho các điểm \(A(2; 3); B(9; 4); M(5; y); P(x; 2)\)

a) Tìm \(y\) để tam giác \(AMB\) vuông tại \(M\)

b) Tìm \(x\) để ba điểm \(A, P\) và \(B \)thẳng hàng

Bài giải:

bài 9 trang 99 hình học 10a) Ta có:

\(\left\{ \matrix{
\overrightarrow {MA} = ( – 3;3 – y) \hfill \cr
\overrightarrow {MB} = (4;4 – y) \hfill \cr} \right.\)

Tam giác \(AMB\) vuông tại \(M\) nên \(\overrightarrow {MA} \bot \overrightarrow {MB} \)

Suy ra:

\(\eqalign{
& – 3.4{\rm{ }} + \left( {3-y} \right)\left( {4-y} \right) = 0 \cr
& \Leftrightarrow {y^2} – 7y = 0 \Leftrightarrow \left[ \matrix{
y = 0 \hfill \cr
y = 7 \hfill \cr} \right. \cr} \)

Vậy \(M(5; 0)\) hoặc \(M(5; \, 7).\)

b) Ta có:

\(\left\{ \matrix{
\overrightarrow {AP} = (x – 2, – 1) \hfill \cr
\overrightarrow {AB} = (7,1) \hfill \cr} \right.\)

Để ba điểm \(A, P\) và \(B\) thẳng hàng thì \(\overrightarrow {AP} = k\overrightarrow {AB} \)

\( \Leftrightarrow \left\{ \matrix{
x – 2 = 7k \hfill \cr
– 1 = k \hfill \cr} \right.\)\( \Leftrightarrow \left\{ \matrix{
x = – 5 \hfill \cr
k = – 1 \hfill \cr} \right. \Rightarrow x = – 5\)

Vậy \(x=-5\) thì \(A, \, P\) và \(B\) thẳng hàng.

7. Giải bài 7 trang 99 sgk Hình học 10

Cho tam giác \(ABC\) với \(H\) là trực tâm. Biết phương trình của đường thẳng \(AB, BH\) và \(AH\) lần lượt là: \(4x + y – 12 = 0, 5x – 4y – 15 = 0\) và \(2x + 2y – 9 = 0\)

Hãy viết phương trình hai đường thẳng chứa hai cạnh còn lại và đường cao thứ ba.

Bài giải:

Tọa độ đỉnh \(A\) là nghiệm của hệ:

\(\left\{ \matrix{
4x + y – 12 = 0 \hfill \cr
2x + 2y – 9 = 0 \hfill \cr} \right. \Rightarrow A({5 \over 2},2)\)

Đường thẳng \(BH : 5x – 4y – 15 = 0\) có vecto chỉ phương \(\overrightarrow u = (4,5)\)

Cạnh \(AC\) vuông góc với \(BH\) nên nhận vecto u làm một vecto pháp tuyến, \(AC\) đi qua \(A({5 \over 2},2)\) và có vecto pháp tuyến \(\overrightarrow u = (4,5)\) nên có phương trình là:

\(4.(x – {5 \over 2}) + 5(y – 2) = 0 \)\(\Leftrightarrow 4x + 5y – 20 = 0\)

Tương tự, tọa độ đỉnh \(B\) là nghiệm của hệ:

\(\left\{ \matrix{
4x + y – 12 = 0 \hfill \cr
6x – 4y – 15 = 0 \hfill \cr} \right. \Rightarrow B(3,0)\)

\(AH: 2x + 2y – 9 = 0\) có vecto chỉ phương \(\overrightarrow v = ( – 2,2) = 2( – 1,1)\)

\(BC\) vuông góc với \(AH\) nên nhận vecto \(\overrightarrow {v’} = ( – 1,1)\) làm vecto pháp tuyến, phương trình \(BC\) là:

\( – 1(x – 3) + (y – 0) = 0 \)\(\Leftrightarrow x – y – 3 = 0\)

Tọa độ \(H\) là nghiệm của hệ phương trình:

\(\left\{ \matrix{
5x – 4y – 15 = 0 \hfill \cr
2x + 2y – 9 = 0 \hfill \cr} \right. \Leftrightarrow H({{11} \over 3},{5 \over 6})\)

Đường cao \(CH\) đi qua \(H\) và vuông góc với \(AB\)

Hoàn toàn tương tự, ta viết được phương trình của \(CH\):

\(CH: 3x – 12y – 1= 0.\)

8. Giải bài 8 trang 99 sgk Hình học 10

Lập phương trình đường tròn có tâm nằm trên đường thẳng \(Δ :4x + 3y – 2 = 0\) và tiếp xúc với hai đường thẳng \(d_1: x + y + 4 = 0\) và \(d_2: 7x – y + 4 = 0.\)

Bài giải:

Ta biết đường tròn tiếp xúc với hai cạnh của một góc tù thì có tâm nằm trên đường phân giác của góc đó.

Tâm \(I\) của đường tròn cần tìm là giao điểm của \(Δ\) với các đường phân giác của các góc đo do hai đường thẳng \(d_1\) và \(d_2\) tạo thành.

Phương trình hai đường thẳng phân giác của các góc do \(d_1\) và \(d_2\) tạo thành là:

\({{x + y + 4} \over {\sqrt {{1^2} + {1^2}} }} = \pm {{7x – y + 4} \over {\sqrt {{7^2} + {1^2}} }}\)

Rút gọn, ta được phương trình hai phân giác:

\(p_1: x – 3y – 8 = 0\)

\(p_2: 3x + y + 6 = 0\)

Tâm \(I \) của đường tròn có tọa độ là nghiệm của hệ:

\((I)\left\{ \matrix{
x – 3y – 8 = 0 \hfill \cr
4x + 3y – 2 = 0 \hfill \cr} \right.;\)

\((II)\left\{ \matrix{
3x + y + 6 = 0 \hfill \cr
4x + 3y – 2 = 0 \hfill \cr} \right.\)

Hệ (I) cho ta nghiệm là \(I_1(2; -2)\)

Hệ (II) cho ta nghiệm là \(I_2(-4; 6)\)

Bán kính \(R\) là khoảng cách từ \(I\) đến một cạnh, tức là đến đường thẳng \(d_1\) (hoặc \(d_2\)) nên:

♦ Với tâm \(I_1 (2; -2)\) \( \Rightarrow {R_1} = {{|2 – 2 + 4|} \over {\sqrt 2 }} = 2\sqrt 2 \)

Và được đường tròn \((C_1): (x – 2)^2+ (y + 2)^2= 8\)

♦ Với tâm \(I_2(-4; 6)\) \( \Rightarrow {R_2} = {{| – 4 + 6 + 4|} \over {\sqrt 2 }} = 3\sqrt 2 \)

Và được đường tròn \((C_2): (x + 4)^2+ (y – 6)^2= 18\)

9. Giải bài 9 trang 99 sgk Hình học 10

Cho elip \((E)\) có phương trình: \({{{x^2}} \over {100}} + {{{y^2}} \over {36}} = 1\)

a) Hãy xác định tọa độ các đỉnh, các tiêu điểm của elip \((E)\) và vẽ elip đó

b) Qua tiêu điểm của elip dựng đường thẳng song song với \(Oy\) và cắt elip tại hai điểm \(M\) và \(N\). Tính độ dài đoạn thẳng \(MN\).

Bài giải:

a) Ta có: \(a^2= 100 ⇒ a = 10\)

\(b^2= 36 ⇒ b = 6\)

\(c^2= a^2– b^2= 64 ⇒ c = 8\)

Từ đó ta được:

\(A_1(-10; 0), A_2(10; 0), B_1(0; -3), \)\(B_2(0;3), F_1(-8; 0), F_2(8; 0)\)

b) Thế \(x = 8\) vào phương trình của elip ta được:

\({{64} \over {100}} + {{{y^2}} \over {36}} = 1 \Rightarrow y = \pm {{18} \over 5}\)

Ta có: \({F_2}M = {{18} \over 5} \Rightarrow MN = {{36} \over 5}\)

Bài trước:

Bài tiếp theo:

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 10 với giải bài 1 2 3 4 5 6 7 8 9 trang 98 99 sgk Hình học 10!

“Bài tập nào khó đã có giaibaisgk.com“