Nội Dung
Hướng dẫn giải Bài Ôn tập cuối năm Giải tích 12. Nội dung bài trả lời câu hỏi ôn tập cuối năm 1 2 3 4 5 6 7 8 9 10 trang 148 sgk Giải tích 12 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập giải tích có trong SGK để giúp các em học sinh học tốt môn toán lớp 12.
Lý thuyết
1. Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
2. Chương 2. Hàm số lũy thừa. Hàm số mũ và Hàm số lôgarit
3. Chương 3. Nguyên hàm – Tích phân và ứng dụng
5. Tóm tắt lý thuyết Giải tích 12






Dưới đây là Hướng dẫn trả lời câu hỏi ôn tập cuối năm 1 2 3 4 5 6 7 8 9 10 trang 148 sgk Giải tích 12. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Câu hỏi Ôn tập cuối năm
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập giải tích 12 kèm câu trả lời chi tiết câu hỏi ôn tập cuối năm 1 2 3 4 5 6 7 8 9 10 trang 148 sgk Giải tích 12 của Bài Ôn tập cuối năm Giải tích 12 cho các bạn tham khảo. Nội dung chi tiết câu trả lời từng câu hỏi các bạn xem dưới đây:

1. Trả lời câu hỏi 1 trang 148 sgk Giải tích 12
Định nghĩa sự đơn điệu (đồng biến, nghịch biến) của một hàm số trên một khoảng.
Trả lời:
Định nghĩa sự đơn điệu (đồng biến, nghịch biến) của một hàm số:
Kí hiệu $K$ là một khoảng, một đoạn hoặc một nửa khoảng.
Cho hàm số \(y=f(x)\) xác định trên $K$.
Hàm số \(y=f(x)\) đồng biến (tăng) trên $K$ nếu \(\left\{ {\begin{array}{*{20}{c}} {{x_1},{x_2} \in K}\\ {{x_1} < {x_2}} \end{array}} \right. \Rightarrow f({x_1}) < f({x_2})\).
Hàm số \(y=f(x)\) nghịch biến (giảm) trên $K$ nếu \(\left\{ {\begin{array}{*{20}{c}} {{x_1},{x_2} \in K}\\ {{x_1} < {x_2}} \end{array}} \right. \Rightarrow f({x_1}) > f({x_2})\).
2. Trả lời câu hỏi 2 trang 148 sgk Giải tích 12
Phát biểu các điều kiện cần và đủ để hàm số f(x) đơn điệu trên một khoảng.
Trả lời:
♦ Điều kiện cần để hàm số đơn điệu:
Cho hàm số \(y=f(x)\) có đạo hàm trên $K$:
– Nếu \(f(x)\) đồng biến trên $K$ thì \(f'(x)\geq 0\) với mọi \(x\in K\).
– Nếu \(f(x)\) nghịch biến trên $K$ thì \(f'(x)\leq 0\) với mọi \(x\in K\).
♦ Điều kiện đủ để hàm số đơn điệu:
Cho hàm số \(y=f(x)\) có đạo hàm trên $K$:
– Nếu \(f'(x)\geq 0\) với mọi \(x\in K\) và \(f'(x)=0\) chỉ tại một số hữu hạn điểm thuộc $K$ thì \(f(x)\) đồng biến trên $K$.
– Nếu \(f'(x)\leq 0\) với mọi \(x\in K\) và \(f'(x)=0\) chỉ tại một số hữu hạn điểm thuộc $K$ thì \(f(x)\) nghịch biến trên $K$.
– Nếu \(f'(x)=0\) với mọi \(x\in K\) thì \(f(x)\) là hàm hằng trên $K$.
3. Trả lời câu hỏi 3 trang 148 sgk Giải tích 12
Phát biểu các điều kiện cần và đủ để hàm số f(x) có cực trị (cực đại, cực tiểu) tại điểm x0.
Trả lời:
♦ Điều kiện cần để hàm số có cực trị
\(f(x)\) đạt cực trị tại \(x_0\), có đạo hàm tại \(x_0\) thì \(f'(x_0)=0\).
♦ Điều kiện đủ để hàm số có cực trị:
Định lí 1. Cho hàm số $y = f(x)$ liên tục trên khoảng $K = (x_0 – h ; x_0 + h) (h > 0)$ và có đạo hàm trên $K$ hoặc trên $K$ \(\setminus\){ x0 }.
– Nếu \(\left\{ \matrix{f’\left( x \right) > 0|\forall \left( {{x_0} – h;\,\,{x_0}} \right) \hfill \cr f’\left( x \right) < 0|\forall \left( {{x_0};\,\,{x_0} + h} \right) \hfill \cr} \right.\) thì x0 là điểm cực đại của hàm số
– Nếu \(\left\{ \matrix{f’\left( x \right) < 0|\forall \left( {{x_0} – h;\,\,{x_0}} \right) \hfill \cr f’\left( x \right) > 0|\forall \left( {{x_0};\,\,{x_0} + h} \right) \hfill \cr} \right.\) thì x0 là điểm cực tiểu của hàm số
Định lí 2. Cho hàm số $y = f(x)$ có đạo hàm cấp hai trên khoảng $K = (x_0 – h ; x_0 + h) (h > 0).$
– Nếu $f'(x_0) = 0, f”(x_0) > 0$ thì $x_0$ là điểm cực tiểu của hàm số $f$.
– Nếu $f'(x_0) = 0, f”(x_0) < 0 thì $x_0$ là điểm cực đại của hàm số $f$.
4. Trả lời câu hỏi 4 trang 148 sgk Giải tích 12
Nêu sơ đồ khảo sát sự biến thiên và vẽ đồ thị của hàm số.
Trả lời:
Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y=f(x)\):
– Bước 1: Tìm tập xác định của hàm số
– Bước 2: Khảo sát sự biến thiên:
Xét chiều biến thiên của hàm số:
Tính đạo hàm \(f'(x)\).
Tìm các điểm mà tại đó \(f'(x)=0\) hoặc không xác định.
Xét dấu đạo hàm \(f'(x)\) và suy ra chiều biến thiên của hàm số.
Tìm cực trị của hàm số.
Tính các giới hạn \(\lim_{x\rightarrow +\infty }y,\lim_{x\rightarrow -\infty }y\) và các giới hạn có kết quả là vô cực (\(= \pm \infty\)), tìm các đường tiệm cận (nếu có)
– Bước 3: Vẽ đồ thị
Xác định các điểm đặc biệt: giao với Ox, Oy điểm có tọa độ nguyên.
Nêu tâm đối xứng, trục đối xứng (nếu có).
Chú ý:
– Đồ thị hàm số bậc ba nhận điểm \(I(x_0,f(x_0))\) với \(x_0\) là nghiệm phương trình \(f”(x_0)=0\) làm tâm đối xứng.
– Đồ thị hàm số phân thức bậc nhất / bậc nhất nhận giao của hai tiệm cận làm tâm đối xứng.
– Đồ thị hàm số lẻ nhận \(O(0;0)\) làm tâm đối xứng.
– Đồ thị hàm số chẵn nhận Oy làm trục đối xứng.
5. Trả lời câu hỏi 5 trang 148 sgk Giải tích 12
Nêu định nghĩa và các tính chất cơ bản của lôgarit.
Trả lời:
– Định nghĩa: Cho hai số thực dương \(a\) và \(b\) với \(a\ne1\). Số \(\alpha\) thỏa mãn \(a^{\alpha}=b\) được gọi là lôgarit có số \(a\) của \(b\), kí hiệu \(\log_ab=\alpha\).
Vậy: \(\alpha = {\log _a}b \Leftrightarrow \left\{ \begin{array}{l} 0 < a \ne 1,b > 0\\ {a^\alpha } = b \end{array} \right.\)
Ví dụ: \(\log_2\sqrt{2}=\frac{1}{2}\) vì \(2^\frac{1}{2}=\sqrt{2}\)
– Tính chất cơ bản của lôgarit: Cho hai số thực dương \(a\) và \(b\) với \(a\ne1\). Ta có các tính chất sau:
\(\begin{array}{l} {\log _a}1 = 0;\,\,{\log _a}a = 1;\\ {a^{{{\log }_a}b}} = b;\,\,{\log _a}\left( {{a^\alpha }} \right) = \alpha . \end{array}\)
6. Trả lời câu hỏi 6 trang 148 sgk Giải tích 12
Phát biểu các định lí về quy tắc tính lôgarit, công thức đổi cơ số của lôgarit.
Trả lời:
♦ Qui tắc tính lôgarit:
Cho số thực \(a\) thỏa \(0< a\neq 1\), ta có các tính chất sau: Với \(b>0\): \(a^{\log_ab}=b\)
– Lôgarit của một tích:
Với \(x_1,x_2>0\): \(\log_a(x_1.x_2)=\log_ax_1+\log_ax_2\)
Mở rộng với \(x_1,x_2,…, x_n>0\): \(\log_a(x_1.x_2….x_n)=\log_ax_1+\log_ax_2+…+\log_ax_n\)
– Lôgarit của một thương:
Với \(x_1,x_2>0 :\ \log_a\frac{x_1}{x_2}=\log_ax_1-\log_ax_2\)
Với \(x> 0: \log_a\frac{1}{x}=-\log_ax\)
– Lôgarit của một lũy thừa:
Với \(b>0:\) \(\log_ab^x=x\log_ab\)
\(\forall x\): \(\log_aa^x=x\)
♦ Công thức đổi cơ số:
Cho số thực \(a\) thỏa \(0< a\neq 1\), ta có các tính chất sau:
\(\log_ab=\frac{\log_c \ b}{\log_c \ a}\)
Lấy \(0 < b \ne 1\), chọn \(c=b\) ta có: \({\log _a}b = \frac{1}{{{{\log }_b}a}}\)
Với \(\alpha \neq 0,b>0\): \(\log_{a^\alpha }b^\beta =\frac{\beta }{\alpha }\log_ab\)
Với \(\alpha \neq 0, b>0:\) \(\log_{a^\alpha }b=\frac{1}{\alpha }\log_ab\)
7. Trả lời câu hỏi 7 trang 148 sgk Giải tích 12
Nêu tính chất của hàm số mũ, hàm số logarit, mối liên hệ giữa đồ thị các hàm số mũ và hàm số logarit cùng cơ số.
Trả lời:
♦ Tính chất hàm số mũ:
– Tập xác định: \(\mathbb{R}.\)
– Tập giá trị: \((0;+\infty )\)
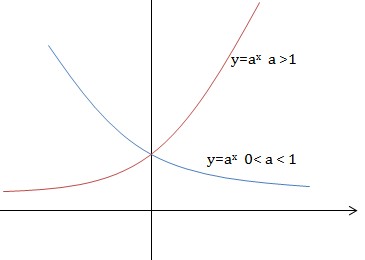
Với \(a>1\) hàm số \(y=a^x\) đồng biến trên \(\mathbb{R}.\)
Với $0< a < 1$ thì hàm số luôn nghịch biến.
– Đồ thị hàm số mũ nhận trục \(Ox\) làm tiệm cận ngang.
♦ Tính chất hàm số Lôgarit:
– Tập xác định: \(\left( {0; + \infty } \right).\)
– Tập giá trị: \(\mathbb{R}.\)
Với \(a>1\): \(y=\log_ax\) là hàm số đồng biến trên \(\left( {0; + \infty } \right).\)
Với 0< a < 1 thì hàm số luôn nghịch biến
Với \(x_1>0,x_2>0\): \(\log_ax_1=\log_ax_2\Leftrightarrow x_1=x_2\)
♦ Mối liên hệ giữa đồ thị các hàm số mũ và hàm số logarit cùng cơ số:
Đồ thị hàm số \(y=a^x\) và đồ thị hàm số \(y=\log_ax\) (cùng cơ số a) luôn đối xứng nhau qua đường thẳng y=x như hình vẽ sau:


8. Trả lời câu hỏi 8 trang 148 sgk Giải tích 12
Nêu định nghĩa và các phương pháp tính nguyên hàm.
Trả lời:
♦ Định nghĩa: Cho hàm số \(f(x)\) xác định trên K.
Hàm số \(F(x)\) được gọi là nguyên hàm của hàm số \(f(x)\) trên K nếu \(F'(x) = f(x)\) với mọi \(x \in K.\)
♦ Phương pháp tính nguyên hàm:
– Phương pháp đổi biến số:
Định lí 1: Cơ sở của phương pháp đổi biến số là định lý sau: Cho hàm số \(u = u(x)\) có đạo hàm và liên tục trên K và hàm số \(y = f({\rm{u)}}\) liên tục sao cho \(f[u(x)]\) xác định trên K. Khi đó nếu \(F\) là một nguyên hàm của \(f\), tức là \(\int {f(u)du = F(u) + C}\) thì \(\int {f[u(x){\rm{]dx = F[u(x)] + C}}}.\)
Hệ quả: Với \(u = ax + b\,(a \ne 0),\) ta có:
\(\int {f(ax + b)dx} = \frac{1}{a}F(ax + b) + C\)
– Phương pháp tính nguyên hàm từng phần:
Định lí 2: Nếu hai hàm số \(u=u(x)\) và \(v=v(x)\) có đạo hàm và liên tục trên K thì:
\(\int {u(x)v'(x)dx} = u(x)v(x) – \int {u'(x)v(x)dx}\)
Một số dạng thường gặp:
– Dạng 1: \(\int {P(x).{e^{{\rm{ax}} + b}}dx\,,\,\,\int {P(x)\sin ({\rm{ax}} + b)dx\,,\,\int {P(x)c{\rm{os}}({\rm{ax}} + b)dx} } }\).
Cách giải: Đặt \(u = P(x)\,,\,dv = {e^{{\rm{ax}} + b}}dx\,\) hoặc \(dv = \sin (ax + b)dx,\,\,dv = \cos (ax + b)dx.\)
– Dạng 2: \(\int {P(x)\ln ({\rm{ax}} + b)dx}\)
Cách giải: Đặt \(u = \ln ({\rm{ax}} + b)\,,\,dv = P(x)dx.\)
9. Trả lời câu hỏi 9 trang 148 sgk Giải tích 12
Nêu định nghĩa và các phương pháp tính tích phân.
Trả lời:
♦ Định nghĩa:
Cho hàm \(f(x)\) liên tục trên khoảng K và a, b là hai số bất kỳ thuộc K. Nếu \(F(x)\) là một nguyên hàm của \(f(x)\) thì hiệu số \(F(b)-F(a)\) được gọi là tích phân của \(f(x)\) từ a đến b và ký hiệu là \(\int\limits_a^b {f(x)dx} .\) Trong trường hợp \(a<b\) thì \(\int\limits_a^b {f(x)dx}\) là tích phân của \(f\) trên \([a;b].\)
♦ Các phương pháp tính tích phân:
– Phương pháp đổi biến số:
Công thức đổi biến số \(\int\limits_a^b {f[u(x)]u'(x)dx = \int\limits_{u(a)}^{u(b)} {f(u)du} }.\) Trong đó \(f(x)\) là hàm số liên tục và \(u(x)\) có đạo hàm liên tục trên khoảng J sao cho hàm hợp \(f[u(x)]\) xác định trên J; \(a,\,b \in J.\)
Các phương pháp đổi biến số thường gặp:
Cách 1: Đặt \(u = u(x)\) (\(u\) là một hàm theo \(x\)).
Cách 2: Đặt \(x=x(t)\) (\(x\) là một hàm theo \(t\)).
– Phương pháp tích phân từng phần:
Định lí: Nếu \(u(x),\,v(x)\) là hai hàm số có đạo hàm liên tục trên khoảng K và \(a,b\) là hai số thuộc K thì \(\int\limits_a^b {u(x)v'(x)dx} = \left. {u(x)v(x)} \right|_a^b – \int\limits_a^b {v(x)u'(x)dx}.\)
10. Trả lời câu hỏi 10 trang 148 sgk Giải tích 12
Nhắc lại các định nghĩa số phức, số phức liên hợp, môđun của số phức. Biểu diễn hình học của số phức.
Trả lời:
Số phức \(z = a + bi\) có phần thực là \(a\), phần ảo là \(b\) (\(a,b\in\mathbb{R}\) và \(i^2=-1\)).
Số phức bằng nhau \(a + bi = c + di \Leftrightarrow\) \(a=c\) và \(b=d.\)
Số phức \(z = a + bi\) được biểu diễn bới điểm \(M(a,b)\) trên mặt phẳng toạ độ.

Độ dài của vectơ OM là môđun của số phức \(z\), kí hiệu là \(\left| z \right| = \overrightarrow {OM} = \sqrt {{a^2} + {b^2}} .\)

Số phức liên hợp của số phức \(z = a + bi\) là \(a-bi\) kí hiệu là \(\overline z = a – bi.\)

Bài trước:
- Ôn tập chương 4: Giải bài 1 2 3 4 5 6 7 8 9 10 11 12 trang 145 146 sgk Giải tích 12
- Ôn tập chương 4: Giải bài tập trắc nghiệm 1 2 3 4 5 6 trang 146 147 sgk Giải tích 12
Bài tiếp theo:
Xem thêm:
- Các bài toán 12 khác
- Để học tốt môn Vật lí lớp 12
- Để học tốt môn Sinh học lớp 12
- Để học tốt môn Ngữ văn lớp 12
- Để học tốt môn Lịch sử lớp 12
- Để học tốt môn Địa lí lớp 12
- Để học tốt môn Tiếng Anh lớp 12
- Để học tốt môn Tiếng Anh lớp 12 thí điểm
- Để học tốt môn Tin học lớp 12
- Để học tốt môn GDCD lớp 12
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 12 với trả lời câu hỏi ôn tập cuối năm 1 2 3 4 5 6 7 8 9 10 trang 148 sgk Giải tích 12!
“Bài tập nào khó đã có giaibaisgk.com“
