Nội Dung
Hướng dẫn giải Bài Ôn tập Chương 4. Số phức, sách giáo khoa Giải tích 12. Nội dung bài giải bài 1 2 3 4 5 6 7 8 9 10 11 12 trang 145 146 sgk Giải tích 12 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập giải tích có trong SGK để giúp các em học sinh học tốt môn toán lớp 12.
Lý thuyết
1. §1. Số phức
2. §2. Cộng, trừ và nhân số phức
4. §4. Phương trình bậc hai với hệ số thực
Dưới đây là Hướng dẫn giải bài 1 2 3 4 5 6 7 8 9 10 11 12 trang 145 146 sgk Giải tích 12. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập Ôn tập chương 4
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập giải tích 12 kèm bài giải chi tiết bài 1 2 3 4 5 6 7 8 9 10 11 12 trang 145 146 sgk Giải tích 12 của Bài Ôn tập Chương 4. Số phức cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
1. Giải bài 1 trang 145 sgk Giải tích 12
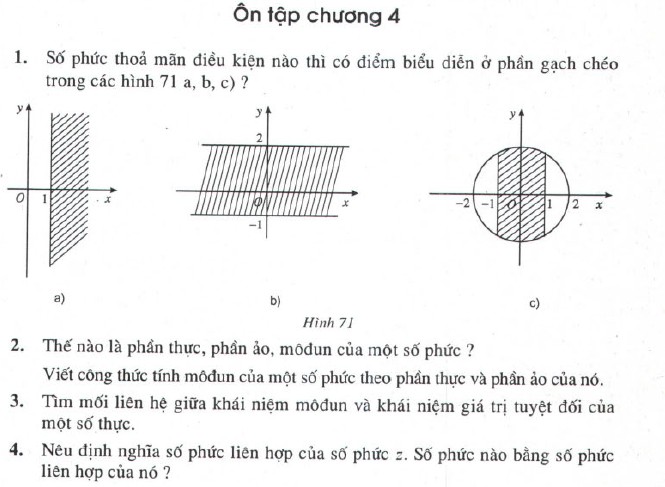
Số phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo trong các hình 71 a), b), c) ?

Bài giải:
Giả sử \(z = x + yi\) (\(x,y \in \mathbb R\)), khi đó số phức \(z\) được biểu diễn bởi điểm \(M(x, y)\) trên mặt phẳng tọa độ \(Oxy\).
a) Trên hình 71.a), tập hợp điểm M biểu diễn cho số phức \(z\) thuộc phần gạch chéo là \(\left\{ {M\left( {x;y} \right)|x \ge 1} \right\}\).
Vậy số phức có phần thực lớn hơn hoặc bằng \(-1\) có điểm biểu diễn ở phần gạch chéo hình 71.a)
b) Trên hình 71.b, tập hợp điểm M biểu diễn cho số phức \(z\) thuộc phần gạch chéo là \(\left\{ {M\left( {x;y} \right)| – 1 \le y \le 2} \right\}\)
Vậy số phức có phần ảo thuộc đoạn \([-1, 2]\) có điểm biểu diễn ở phần gạch chéo hình 71.b)
c) Trên hình 71.c), tập hợp điểm M biểu diễn cho số phức \(z\) thuộc phần gạch chéo là \(\left\{ {M\left( {x;y} \right)|{x^2} + {y^2} = 4, – 1 \le x \le 1} \right\}\).
Vậy số phức có phần thực thuộc đoạn \([-1, 1]\) và môdun không vượt quá \(2\) có điểm biểu diễn ở phần gạch chéo hình 71.c).
2. Giải bài 2 trang 145 sgk Giải tích 12
Thế nào là phần thực, phần ảo, modun của số phức?
Viết công thức tính môdun của một số phức theo phần thực và phần ảo của nó.
Bài giải:
Mỗi biểu thức dạng \(a+bi\), trong đó \(a, b ∈ R, i^2= -1\) được gọi làm một số phức.
Với số phức \(z = a + bi\), ta gọi \(a\) là phần thực, số \(b\) gọi là phần ảo của \(z\).
Ta có \(z = a + bi\) thì môdun của \(z\) là \(|z| = |a + bi| = \sqrt {{a^2} + {b^2}} \).
3. Giải bài 3 trang 145 sgk Giải tích 12
Tìm mối liên hệ giữa khái niệm môdun và khái niệm giá trị tuyệt đối của một số thực.
Bài giải:
Nếu số thực \(z\) là một số thực thì môdun \(x\) chính là giá trị tuyệt đối của số phức \(z\).
Nếu số phức \(z\) không phải là một số thực, \(z=a+bi\) \((a,b \in R\)) thì chỉ có môdun của \(z\) bằng: \(\left| z \right| = \sqrt {{a^2} + {b^2}} \), không có khái niệm giá trị tuyệt đối của số phức \(z\).
4. Giải bài 4 trang 145 sgk Giải tích 12
Nêu định nghĩa số phức liên hợp của số phức \(z\). Số phức nào bằng số phức liên hợp của nó?
Bài giải:
Cho số phức \(z = a + bi\).
Ta gọi số phức \(a – bi\) là số phức liên hợp của \(z\) và kí hiệu là \(\bar z\).
Vậy ta có \(z = a + bi\) thì \(\bar z= a – bi\)
Số phức \(z\) bằng số phức liên hợp của nó \(⇔ a = a\) và \(b = -b\)
\(⇔ a ∈ R\) và \(b = 0 ⇔ z\) là một số thực.
5. Giải bài 5 trang 146 sgk Giải tích 12
Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức \(z\) thỏa mãn điều kiện:
a) Phần thực của \(z\) bằng \(1\);
b) Phần ảo của \(z\) bằng \(-2\);
c) Phần thực của \(z\) thuộc đoạn \([-1, 2]\), phần ảo của \(z\) thuộc đoạn \([0, 1]\);
d) \(|z| ≤ 2\).
Bài giải:
Tập hợp các điểm biểu diễn các số phức $z$ là các hình sau:
a) Ta có \(x = 1, y\) tùy ý nên tập hợp các điểm biểu diễn \(z\) là đường thẳng \(x = 1\).

b) Ta có \(y = -2, x\) tùy ý nên tập hợp các điểm biểu diễn \(z\) là đường thẳng \(y = -2\).

c) Ta có \(x \in \left[ { – 1;2} \right]\), tức là \( – 1 \le x \le 2\), tập hợp các điểm M nằm bên trái đường thẳng \(x=2\) và nằm bên phải đường thẳng \(x=-1\) và \(y ∈ [0, 1]\), tức là \(0 \le y \le 1\) tập hợp các điểm M nằm bên dưới đường thẳng \(y=1\) và nằm bên trên đường thẳng \(y=0\).
Vậy tập hợp các điểm biểu diễn \(z\) là hình chữ được tô màu.

d) Ta có:
\(\left| z \right| \le 2 \Leftrightarrow \sqrt {{x^2} + {y^2}} \le 2 \Leftrightarrow {x^2} + {y^2} \le 4\)
Vậy tập hợp các điểm biểu diễn \(z\) là hình tròn tâm \(O\) (gốc tọa độ) bán kính bằng \(2\) (kể cả các điểm trên đường tròn).

6. Giải bài 6 trang 146 sgk Giải tích 12
Tìm các số thực \(x, y\) sao cho:
a) \(3x + yi = 2y + 1 + (2-x)i\);
b) \(2x + y – 1 = (x – 2y – 5)i\)
Bài giải:
a) Ta có:
\(\eqalign{
& 3x + yi = (2y + 1)+(2 – x)i \cr
& \Leftrightarrow \left\{ \matrix{
3x = 2y + 1 \hfill \cr
y = 2 – x \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 1 \hfill \cr
y = 1 \hfill \cr} \right. \cr} \)
b) Ta có:
\(\eqalign{
& 2x + y – 1 = (x + 2y – 5)i \cr
& \Leftrightarrow \left\{ \matrix{
2x + y – 1 = 0 \hfill \cr
x + 2y – 5 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = – 1 \hfill \cr
y = 3 \hfill \cr} \right. \cr} \)
7. Giải bài 7 trang 146 sgk Giải tích 12
Chứng tỏ rằng với mọi số phức \(z\), ta luôn có phần thực và phần ảo của \(z\) không vượt quá môdun của nó.
Bài giải:
Giả sử \(z = a + bi\)
Khi đó: \(\left| z \right| = \sqrt {{a^2} + {b^2}}\)
Từ đó suy ra:
\(|z| \ge \sqrt {{a^2}} = |a| \ge a,|z| \ge \sqrt {{b^2}} = |b| \ge b\)
8. Giải bài 8 trang 146 sgk Giải tích 12
Thực hiện các phép tính sau:
a) \((3 + 2i)[(2 – i) + (3 – 2i)]\)
b) \((4 – 3i) + {{1 + i} \over {2 + i}}\)
c) \((1 + i)^2 – (1 – i)^2\)
d) \({{3 + i} \over {2 + i}} – {{4 – 3i} \over {2 – i}}\)
Bài giải:
a) Ta có:
\((3 + 2i)[(2 – i) + (3 – 2i)]= (3 + 2i)(5 – 3i) = 21 + i\)
b) Ta có:
\(\eqalign{
& (4 – 3i) + {{1 + i} \over {2 + i}} = (4 – 3i) + {{(1 + i)(2 – i)} \over 5} = (4 – 3i)({3 \over 5} + {1 \over 5}i) \cr
& = (4 + {3 \over 5}) – (3 – {1 \over 5})i = {{23} \over 5} – {{14} \over 5}i \cr} \)
c) Ta có:
\((1 + i)^2 – (1 – i)^2 = 2i – (-2i) = 4i\)
d) Ta có:
\(\eqalign{
& {{3 + i} \over {2 + i}} – {{4 – 3i} \over {2 – i}} = {{(3 + i)(2 – i)} \over 5} – {{(4 – 3i)(2 + i)} \over 5} \cr
& = {{7 – i} \over 5} – {{11 – 2i} \over 5} = {{ – 4} \over 5} + {1 \over 5}i \cr} \)
9. Giải bài 9 trang 146 sgk Giải tích 12
Giải các phương trình sau trên tập số phức:
a) \((3 + 4i)z + (1 – 3i) = 2 + 5i\);
b) \((4 + 7i)z – (5 – 2i) = 6iz\).
Bài giải:
\(\begin{array}{l}
a)\,\,\left( {3 + 4i} \right)z + \left( {1 – 3i} \right) = 2 + 5i\\
\Leftrightarrow \left( {3 + 4i} \right)z = 2 + 5i – \left( {1 – 3i} \right)\\
\Leftrightarrow \left( {3 + 4i} \right)z = 1 + 8i \Leftrightarrow z = \frac{{1 + 8i}}{{3 + 4i}}\\
\Leftrightarrow z = \frac{{\left( {1 + 8i} \right)\left( {3 – 4i} \right)}}{{{3^2} + {4^2}}} \Leftrightarrow z = \frac{{35 + 20i}}{{25}} \Leftrightarrow z = \frac{7}{5} + \frac{4}{5}i\\
b)\,\,\left( {4 + 7i} \right)z – \left( {5 – 2i} \right) = 6iz\\
\Leftrightarrow \left( {4 + 7i} \right)z – 6iz = 5 – 2i\\
\Leftrightarrow \left( {4 + i} \right)z = 5 – 2i \Leftrightarrow z = \frac{{5 – 2i}}{{4 + i}}\\
\Leftrightarrow z = \frac{{\left( {5 – 2i} \right)\left( {4 – i} \right)}}{{{4^2} + {1^2}}}\\
\Leftrightarrow z = \frac{{18 – 13i}}{{17}} = \frac{{18}}{{17}} – \frac{{13}}{{17}}i
\end{array}\)
10. Giải bài 10 trang 146 sgk Giải tích 12
Giải các phương trình sau trên tập số phức
a) \(3z^2+ 7z + 8 = 0\);
b) \(z^4– 8 = 0\);
c) \(z^4– 1 = 0\).
Bài giải:
a) \(3z^2+ 7z + 8 = 0\) có \(Δ = 49 – 4.3.8 = -47\)
Vậy phương trình có hai nghiệm là: \({z_{1,2}} = {{ – 7 \pm i\sqrt {47} } \over 6}\)
b) \(z^4– 8 = 0\)
Đặt \(Z = z^2\), ta được phương trình : \(Z^2 – 8 = 0\)
Suy ra: \(Z = ± \sqrt8\)
Vậy phương trình đã cho có 4 nghiệm là: \({z_{1,2}} = \pm \root 4 \of 8 ,{z_{3,4}} = \pm i\root 4 \of 8 \)
c) \(z^4– 1 = 0\)\( ⇔ (z^2– 1)(z^2+ 1) = 0\)
Vậy phương trình đã cho có 4 nghiệm là \(±1\) và \(±i\)
11. Giải bài 11 trang 146 sgk Giải tích 12
Tìm hai số phức, biết tổng của chúng bằng \(3\) và tích của chúng bằng \(4\).
Bài giải:
Giả sử hai số cần tìm là \(z_1\) và \(z_2\).
Ta có: \(z_1 + z_2 = 3\); \(z_1. z_2 = 4\)
Rõ ràng, \(z_1, z_2\) là các nghiệm của phương trình:
\((z – z_1)(z – z_2) = 0\) hay \(z^2– (z_1 + z_2)z + z_1. z_2 = 0\)
Vậy \(z_1, z_2\) là các nghiệm của phương trình: \(z^2 – 3z + 4 = 0\)
Phương trình có \(Δ = 9 – 16 = -7\)
Vậy hai số phức cần tìm là: \({z_1} = {{3 + i\sqrt 7 } \over 2},{z_2} = {{3 – i\sqrt 7 } \over 2}\)
12. Giải bài 12 trang 146 sgk Giải tích 12
Cho hai số phức \(z_1, z_2\). Biết rằng \(z_1 + z_2\) và \(z_1. z_2\) là hai số thực. Chứng minh rằng \(z_1, z_2\) là hai nghiệm của một phương trình bậc hai với hệ số thực.
Bài giải:
Đặt \(z_1 + z_2 = a\); \(z_1. z_2 = b; a, b ∈ \mathbb R\)
Khi đó, \(z_1\) và \(z_2\) là hai nghiệm của phương trình
\((z – z_1)(z – z_2) = 0\) hay \(z^2– (z_1 + z_2)z + z_1. z_2 = 0 ⇔ z^2 – az + b = 0\)
Đó là phương trình bậc hai đối với hệ số thực. Suy ra điều phải chứng minh.
Bài tập trắc nghiệm

1. Giải bài 1 trang 146 sgk Giải tích 12
Số nào trong các số sau là số thực?
(A) \((\sqrt3 + 2i) – (\sqrt3 – 2i)\);
(B) \((2 + i\sqrt5) + (2 – i\sqrt5)\);
(C) \((1 + i\sqrt3)^2\);
(D) \({{\sqrt 2 + i} \over {\sqrt 2 – i}}\).
Trả lời:
Ta tìm phần ảo của các số đã cho:
(A) \((\sqrt3 + 2i) – (\sqrt3 – 2i)\) có phần ảo là \(4i\)
(B) \((2 + i\sqrt5) + (2 – i\sqrt5)\) có phần ảo là \(0\)
(C) \((1 + i\sqrt3)^2\) có phần ảo là \(2\sqrt3\)
(D) \({{\sqrt 2 + i} \over {\sqrt 2 – i}}\) có phần ảo là \({2 \over 3}\sqrt 2 \)
⇒ Chọn đáp án: (B).
2. Giải bài 2 trang 147 sgk Giải tích 12
Số nào trong các số sau là số thuần ảo?
(A)\((\sqrt2+ 3i) – (\sqrt2 + 3i)\);
(B) \((\sqrt2+ 3i) . (\sqrt2 + 3i)\);
(C) \((2 + 2i)^2\);
(D) \({{2 + 3i} \over {2 – 3i}}\).
Trả lời:
Ta tìm phần thực của các số đã cho:
(A) \(\left( {\sqrt 2 + 3i} \right) + \left( {\sqrt 2 – 3i} \right) = \sqrt 2 + 3i + \sqrt 2 – 3i = 2\sqrt 2 \) là số thực.
(B) \(\left( {\sqrt 2 + 3i} \right)\left( {\sqrt 2 – 3i} \right) = {\left( {\sqrt 2 } \right)^2} – {\left( {3i} \right)^2} = 2 + 9 = 11\) là số thực.
(C) \({\left( {2 + 2i} \right)^2} = 4 + 8i – 4 = 8i\) là số thuần ảo.
(D) \(\frac{{2 + 3i}}{{2 – 3i}} = \frac{{{{\left( {2 + 3i} \right)}^2}}}{{\left( {2 – 3i} \right)\left( {2 + 3i} \right)}} = \frac{{4 + 12i – 9}}{{4 + 9}} = \frac{{ – 5}}{{13}} + \frac{{12}}{{13}}i\)
⇒ Chọn đáp án: (C).
3. Giải bài 3 trang 147 sgk Giải tích 12
Đẳng thức nào trong các đẳng thức sau là đúng?
(A) \({i^{1997}}= -1\) ;
(B) \({i^{2345}} = {\rm{ }} i\) ;
(C) \({i^{2005}} = 1\) ;
(D) \({i^{2006}} = {\rm{ }} – i\).
Trả lời:
Ta có:
(A) \({i^{1997}}{\rm{ }} = {\rm{ }}{i^{1976 + 1}}{\rm{ }} = {\rm{ }}{({i^4})^{494}}.i{\rm{ }} = {\rm{ }}i{\rm{ }} \ne {\rm{ }} – 1\)
(B). \({i^{2345}} = {\rm{ }}{i^{2344 + 1}} = {\rm{ }}{({i^4})^{586}}.i{\rm{ }} = {\rm{ }}i\)
(C) \({i^{2005}} = {\rm{ }}{i^{2004 + 1}} = {\rm{ }}{({i^4})^{501}}.i{\rm{ }} = {\rm{ }}i{\rm{ }} \ne {\rm{ }}1\)
(D) \({i^{2006}} = {\rm{ }}{({i^4})^{501}}.({i^2}){\rm{ }} = {\rm{ }} – 1{\rm{ }} \ne {\rm{ }} – i\)
⇒ Chọn đáp án: (B).
4. Giải bài 4 trang 147 sgk Giải tích 12
Đẳng thức nào trong các đẳng thức sau là đúng?
(A) \({\left( {1 + i} \right)^{8}} =- 16\) ;
(B) \({\left( {1 + i} \right)^{8}} =16i\) ;
(C) \({\left( {1 + i} \right)^{8}} = 16\) ;
(D) \({\left( {1 + i} \right)^{8}} =- 16i\).
Trả lời:
Tiến hành tính lần lượt ta có:
\((1+i)^2= 2i ⇒ (1 + i)^4= -4\)
\(⇒ (1 + i)^8= 16\)
⇒ Chọn đáp án: (C).
5. Giải bài 5 trang 147 sgk Giải tích 12
Biết rằng nghịch đảo của số phức \(z\) bằng số phức liên hợp của nó, trong các kết luận sau, kết luận nào là đúng?
(A) \(z ∈ R\) ;
(B) \(|z| = 1\) ;
(C) \(z\) là một số thuần ảo ;
(D) \(|z| = -1\).
Trả lời:
Ta có:
\({1 \over z} = \bar z \Rightarrow z.\bar z = 1 \Rightarrow |z| = 1\)
⇒ Chọn đáp án: (B).
6. Giải bài 6 trang 147 sgk Giải tích 12
Trong các kết luận sau, kết luận nào là sai?
(A) Môdun của số phức \(z\) là một số thực;
(B) Môdun của số phức \(z\) là một số phức;
(C) Môdun của số phức \(z\) là một số thực dương;
(D) Môdun của số phức \(z\) là một số thực không âm.
Trả lời:
Ta có:
\(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \ge 0\).
Môdun của số phức là một số phức không âm nên nó có thể bằng \(0\).
⇒ Chọn đáp án: (C).
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 12 khác
- Để học tốt môn Vật lí lớp 12
- Để học tốt môn Sinh học lớp 12
- Để học tốt môn Ngữ văn lớp 12
- Để học tốt môn Lịch sử lớp 12
- Để học tốt môn Địa lí lớp 12
- Để học tốt môn Tiếng Anh lớp 12
- Để học tốt môn Tiếng Anh lớp 12 thí điểm
- Để học tốt môn Tin học lớp 12
- Để học tốt môn GDCD lớp 12
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 12 với giải bài 1 2 3 4 5 6 7 8 9 10 11 12 trang 145 146 sgk Giải tích 12!
“Bài tập nào khó đã có giaibaisgk.com“
