Giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 trang 88 89 90 sgk Toán 7 tập 2

Nội Dung

Bài ôn cuối năm phần đại số, sách giáo khoa toán 7 tập hai. Nội dung giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 trang 88 89 90 sgk toán 7 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần đại số có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 7.

Lý thuyết

1. Chương I. Số hữu tỉ – Số thực

2. Chương II. Hàm số và đồ thị

3. Chương III – Thống kê

4. Chương IV – Biểu thức đại số

Dưới đây là Hướng dẫn giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 trang 88 89 90 sgk toán 7 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập ôn cuối năm phần Đại số

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần đại số 7 kèm bài giải chi tiết bài 1 2 3 4 5 6 7 8 9 10 11 12 13 trang 88 89 90 sgk toán 7 tập 2 của Bài ôn tập chương III – Thống kê cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 trang 88 89 90 sgk toán 7 tập 2

1. Giải bài 1 trang 88 sgk Toán 7 tập 2

Thực hiện các phép tính:

a) \(9,6.2{1 \over 2} – \left( {2.125 – 1{5 \over {12}}} \right):{1 \over 4}\)

b) \({5 \over {18}} – 1,456:{7 \over {25}} + 4,5.{4 \over 5}\);

c) \(\left( {{1 \over 2} + 0,8 – 1{1 \over 3}} \right).\left( {2,3 + 4{7 \over {25}} – 1,28} \right)\)

d) \(\left( { – 5} \right).12:\left[ {\left( { – {1 \over 4}} \right) + {1 \over 2}:\left( { – 2} \right)} \right] + 1{1 \over 3}\).

Bài giải:

a) \(9,6.2{1 \over 2} – \left( {2.125 – 1{5 \over {12}}} \right):{1 \over 4}\)

\( = 9,6.{5 \over 2} – \left( {250 – {{17} \over {12}}} \right) \times 4\)

\( = 4,8.5 – \left( {1000 – {{17} \over 3}} \right)\)

\( = 24 – 1000 + {{17} \over 3}\)

\( = – 976 + {{17} \over 3}\)

\( = – 970{1 \over 3}\)

b) \({5 \over {18}} – 1,456:{7 \over {25}} + 4,5.{4 \over 5}\);

\( = {5 \over {18}} – 1,456 \times {{25} \over 7} + {9 \over 2}.{4 \over 5}\)

\( = {5 \over {18}} – 0,208 \times 25 + {{18} \over 5}\)

\( = {5 \over {18}} – 5,2 + {{18} \over 5}\)

\( = {{25 – 468 + 324} \over {90}}\)

\( = {{ – 119} \over {90}}\)

c) \(\left( {{1 \over 2} + 0,8 – 1{1 \over 3}} \right).\left( {2,3 + 4{7 \over {25}} – 1,28} \right)\)

\( = \left( {{1 \over 2} + {4 \over 5} – {4 \over 3}} \right).\left( {{{23} \over {10}} + {{107} \over {25}} – {{32} \over {25}}} \right)\)

\( = \left( {{{15 + 24 – 40} \over {30}}} \right).\left( {{{23} \over {10}} + {{107} \over {25}} – {{32} \over {25}}} \right)\)

\( = \left( {{{15 + 24 – 40} \over {30}}} \right).\left( {{{115 + 214 – 64} \over {50}}} \right)\)

\( = {{ – 1} \over {30}}.{{265} \over {50}}\)

\( = {{ – 53} \over {300}}\)

d) \(\left( { – 5} \right).12:\left[ {\left( { – {1 \over 4}} \right) + {1 \over 2}:\left( { – 2} \right)} \right] + 1{1 \over 3}\)

\( = – 60:\left[ {{1 \over 4} + {1 \over 2} \times \left( {{{ – 1} \over 2}} \right)} \right] + 1.{1 \over 3}\)

\( = – 60:\left[ { – {1 \over 4} – {1 \over 4}} \right] + 1{1 \over 3}\)

\( = – 60:\left( {{1 \over 2}} \right) + 1{1 \over 3}\)

\( = 120 + 1{1 \over 3}\)

\( = 121{1 \over 3}\)

2. Giải bài 2 trang 89 sgk Toán 7 tập 2

Với giá trị nào của x thì ta có:

a)|x| + x = 0; b) x + |x| = 2x.

Bài giải:

a) Ta có:

♦ Với thì |x| = x

Khi đó |x| + x = 0 ⇒ x + x = 0 hay 2x = 0 ⇒x = 0 (nhận) (1)

♦ Với x < 0 thì |x| = -x

Khi đó |x| + x = 0 ⇒ -x + x =0

Hay 0x = 0

Biến thức 0x = 0 luôn luôn có nghiệm đúng với mọi x ∈ R

Vì x < 0 nên ta chỉ chọn các giá trị âm của tập số thực R (2)

Từ (1) và (2) ta kết luận: Với mọi giá trị thì: ta có: |x| + x = 0

b) Ta có:

♦ Với x ≥ 0 thì |x| = x

Khi đó từ biểu thức x + |x| = 2x ta được x + x = 2x

Hay 2x = 2x ⇒ 0x = 0

Đẳng thức này luôn có nghiệm đúng với mọi x ∈ R, x ≥ 0 (1)

♦ Với x < 0 thì |x| = -x

Khi đó: x + |x| = 2x ⇒ x – x = 2x hay 2x = 0 ⇒ x = 0 (loại) (2)

Từ (1) và (2) suy ra:

Với mọi giá trị x ∈ R, x ≥ 0 thì ta có biểu thức: x + |x| = 2x

3. Giải bài 3 trang 89 sgk Toán 7 tập 2

Từ tỉ lệ thức \({a \over b} = {c \over d}\left( {a \ne c,b \ne \pm d} \right)\) hãy rút ra tỉ lệ thức: \({{a + c} \over {a – c}} = {{b + d} \over {b – d}}\)

Bài giải:

Áp dụng tính chất tỉ lệ thức ta có:

\({a \over b} = {c \over d} = > {a \over b} = {{a + c} \over {b + d}} = {{a – c} \over {b – d}}\)

\( \Rightarrow {{a + c} \over {b + d}} = {{a – c} \over {b – d}}\)

\( \Rightarrow {{a + c} \over {a – c}} = {{b + d} \over {b – d}}\)

4. Giải bài 4 trang 89 sgk Toán 7 tập 2

Ba đơn vị kinh doanh đầu tư vốn tỉ lệ với 2:5 và 7. Hỏi mỗi đơn vị được chia bao nhiêu lãi nếu số tiền lãi là 560 triệu đồng và tiền lãi được chia tỉ lệ thuận với vốn đầu tư?

Bài giải:

Gọi a, b, c là tiền lãi của mỗi đơn vị.

Vì tiền lãi được chia tỉ lệ với vốn đầu tư nên a, b, c tỉ lệ với 2, 5 và 7 do đó:

\({a \over 2} = {b \over 5} = {c \over 7}\) và a +b +c = 560

\( \Rightarrow {a \over 2} = {b \over 5} = {c \over 7} = {{a + b + c} \over {2 + 5 + 7}} = {{560} \over {14}} = 40\)

Suy ra: a = 2.40 = 80

b = 5.40 =200

c = 7.40 = 280

Vậy số tiền lãi của mỗi đơn vị lần lượt là 80 triệu, 200 triệu, 280 triệu.

5. Giải bài 5 trang 89 sgk Toán 7 tập 2

Chia hàm số: \(y = – 2x + {1 \over 3}\). Các điểm sau đây có thuộc đồ thị hàm số không?

\(A\left( {0;{1 \over 3}} \right);B\left( {{1 \over 2}; – 2} \right);C\left( {{1 \over 6};0} \right)\).

Bài giải:

Gọi (d) là đồ thị của hàm số : \(y = – 2x + {1 \over 3}\)

♦ Với điểm \(A\left( {0;{1 \over 3}} \right)\), ta có:

\(\left. {\matrix{{{y_A} = {1 \over 3}} \cr { – 2{x_A} + {1 \over 3} = – 2.0 + {1 \over 3} = {1 \over 3}} \cr} } \right\} \Rightarrow {y_A} = – 2{x_A} + {1 \over 3}\)

Vậy \(A\left( {0,{1 \over 3}} \right) \in \left( d \right)\)

♦ Với điểm \(B\left( {{1 \over 2}; – 2} \right)\)

\(\left. {\matrix{{{y_B} = – 2} \cr { – 2{x_B} + {1 \over 3} = – 2.{1 \over 2} + {1 \over 3} = – 1 + {1 \over 3} = – {2 \over 3}} \cr} } \right\} \Rightarrow {y_B} \ne – 2{x_B} + {1 \over 3}\)

Vậy \(B\left( {{1 \over 2}; – 2} \right) \notin \left( d \right)\)

♦ Với điểm \(C\left( {{1 \over 6};0} \right)\)

\(\left. {\matrix{{{y_C} = 0} \cr { – 2{x_C} + {1 \over 3} = 2.{1 \over 6} + {1 \over 3} = – {1 \over 3} + {1 \over 3} = 0} \cr} } \right\} \Rightarrow {y_C} = – 2{x_C} + {1 \over 3}\)

Vậy \(C\left( {{1 \over 6};0} \right) \in d\)

6. Giải bài 6 trang 89 sgk Toán 7 tập 2

Biết rằng đồ thị của hàm số y = ax đi qua điểm M(-2;-3). Hãy tìm a.

Bài giải:

Gọi (d) là đồ thị của hàm số y = ax. Vì M(-2;-3) ∈ (d) nên y_M = ax_M.

Hay – 3 = a(-2) ⇒ a =\({3 \over 2}\).

Vậy a = \({3 \over 2}\)

7. Giải bài 7 trang 89 sgk Toán 7 tập 2

Biểu đồ dưới đây biểu diễn tỉ lệ (%) trẻ em từ 6 đến 10 tuổi đang học Tiểu học ở một số vùng của nước ta:

Hãy cho biết:

a) Tỉ lệ (%) trẻ em từ 6 tuổi đến 10 tuổi của vùng Tây Nguyên, vùng đồng bằng sông Cửu Long đi học Tiểu học.

b) Vùng nào có tỉ lệ (%) trẻ em từ 6 tuổi đến 10 tuổi đi học Tiểu học cao nhất, thấp nhất.

Bài giải:

a) Ý nghĩa của các con số ở trục hoành:

Các con số trên trục hoành mang ý nghĩa chỉ số trẻ em (từ 0 em đến 100 em) trong độ tuổi từ 6 đến 10 tuổi ở một vùng trên đất nước ta.

b) Tỉ lệ trẻ em từ 6 đến 10 tuổi của vùng Tây Nguyên đi học đạt 92,29% (so với dân số trong độ tuổi).

Tỉ lệ trẻ em từ 6 đến 10 tuổi của vùng đồng bằng sông Cửu Long đi học đạt 87,81% (so với dân số trong độ tuổi).

c) Đưa vào biểu đồ ta nhận thấy.

Vùng đồng bằng sông Hồng có tỉ lệ trẻ em từ 6 – 10 tuổi đi học tiểu học cao nhất và vùng đồng bằng sông Cửu Long có tỉ lệ trẻ em từ 6 – 10 tuổi đi học tiểu học thấp nhất.

8. Giải bài 8 trang 90 sgk Toán 7 tập 2

Để tìm hiểu về sản lượng vụ mùa của một xã, người ta chọn 120 thửa để gặt thử và ghi lại sản lượng của từng thửa (tính theo tạ/ha). Kết quả được tạm sắp xếp như sau:

Có 10 thửa đạt năng suất 31 tạ/ha; Có 20 thửa đạt năng suất 34 tạ/ha

Có 30 thửa đạt năng suất 35 tạ/ha; Có 15 thửa đạt năng suất 36 tạ/ha

Có 10 thửa đạt năng suất 42 tạ/ha; Có 10 thửa đạt năng suất 40 tạ/ha

Có 5 thửa đạt năng suất 42 tạ/ha; Có 20 thửa đạt năng suất 44 tạ/ha.

a) Dấu hiệu ở đây là gì? Hãy lập bảng “tần số”.

b) Biểu diễn bằng biểu đồ đoạn thẳng.

c) Tìm mốt của dấu hiệu.

d) Tính số trung bình cộng của dấu hiệu.

Bài giải:

a) Dấu hiệu : Sản lượng vụ mùa của mỗi thửa ruộng

Bảng tần số

Năng suất tạ/ha	31	34	35	36	38	40	42	44
Tần số	10	20	30	15	10	10	5	20	N=120

b) Biểu đồ đoạn thẳng

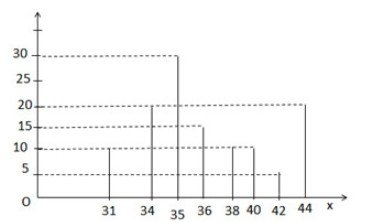
c) Mốt là giá trị có tần số lớn nhất trong bảng tần số. Vậy mốt của dấu hiệu là 35 tạ/ha.

d) Số trung bình cộng của các giá trị

\(\bar X = {{31.10 + 34.20 + 35.30 + 36.15 + 38.10 + 40.10 + 42.5 + 44.20} \over {120}}\)

\(\bar X = {{4450} \over {120}} ⇒ \bar X \approx 37,1\) (tạ/ha)

9. Giải bài 9 trang 90 sgk Toán 7 tập 2

Tính giá trị của biểu thức 2,7c² – 3,5c lần lượt tại c = 0,7; \({2 \over 3};1{1 \over 6}\)

Bài giải:

Đặt A = 2,7c² – 3,5c

♦ Với c = 0,7 ta có :

A = 2,7.(0,7)² – 3,5.0,7 = 2,7.0,49 – 3,5.0,7 = 1,323 – 2,45 = – 1,127

♦ Với c = \({2 \over 3}\) ta có:

\(A = 2,7.{\left( {{2 \over 3}} \right)^2} – 3,5.\left( {{2 \over 3}} \right) = 2,7.{4 \over 9} – 3,5.{2 \over 3}\)

\( = {{10,8} \over 9} – {7 \over 3} = {{10,8 – 21} \over 9} = {{ – 10,2} \over 9}\)

♦ Với c = \(1{1 \over 6} = {7 \over 6}\), ta có:

\(A = 2,7.{({7 \over 6})^2} – 3,5.({7 \over 6}) = 2,7.{{49} \over {36}} – 3,5.{7 \over 6}\)

\( = {{132,3} \over {36}} – {{24,5} \over 6} = {{132,3 – 147} \over {36}} = {{ – 14,7} \over {36}} = {{ – 4,9} \over {12}}\)

10. Giải bài 10 trang 90 sgk Toán 7 tập 2

Cho các đa thức

A = x² – 2x – y² + 3y – 1

B = -2x² + 3y² – 5x + y + 3

C = 3x² – 2xy + 7y² – 3x – 5y – 6

Tính:

a) A + B – C;

b) A – B + C;

c)-A + B + C.

Bài giải:

Có hai cách trình bày với bài này: một là bạn có thể liệt kê hết các phần tử ra hoặc bạn sắp xếp theo cùng thứ tự và tính như sau:

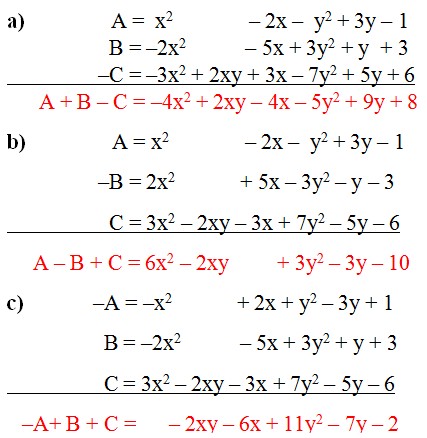
11. Giải bài 11 trang 90 sgk Toán 7 tập 2

Tìm x, biết:

a) (2x – 3) – (x – 5) = (x + 2) – (x – 1).

b) 2(x – 1) – 5(x + 2) = -10

Bài giải:

a) (2x – 3) – (x – 5) = (x + 2) – (x – 1).

2x – 3 – x + 5 = x +2 – x +1

⇒ x +2 =3

⇒ x = 3 – 2

⇒ x = 1

Vậy x = 1

b) 2(x – 1) – 5(x + 2) = -10

⇒ 2x – 2 – 5x -10 = -10

⇒ 2x – 5x = -10 + 10 + 2

⇒ -3x = 2

⇒ x = \({{ – 2} \over 3}\)

Vậy x = \({{ – 2} \over 3}\)

12. Giải bài 12 trang 90 sgk Toán 7 tập 2

Tìm hệ số a của đa thức P(x) =ax² + 5x + 3, biết rằng đa thức này có một nghiệm là \({1 \over 2}\)

Bài giải:

P(x) có nghiệm là \({1 \over 2}\) tức là P(\({1 \over 2}\)) = 0 do đó:

\(a.{1 \over 4} + 5.{1 \over 2} – 3 = 0\)

⇒ \(a.{1 \over 4} = 3 – {5 \over 2}\)

⇒ \(a{1 \over 4} = {1 \over 2}\)

⇒ \(a = {1 \over 2}.4\)

⇒ a = 2

Vậy đa thức P(x) =2x² + 5x – 3

13. Giải bài 13 trang 90 sgk Toán 7 tập 2

a) Tìm nghiệm của đa thức: P(x) = 3 – 2x;

b) Hỏi đa thức Q(x) =x² +2 có nghiệm hay không ? Vì sao?

Bài giải:

a) Ta có: P(x) = 0 khi 3 – 2x = 0

⇒ -2x = -3 ⇒ x = \({3 \over 2}\)

b) Q(x) =x² +2 là đa thức không có nghiệm vì x² ≥ 0

2 > 0 (theo quy tắc nhân hai số hữu tỉ cùng dấu)

⇒ x² + 2 > 0 với mọi x

Nên Q(x) không có nghiệm trong R

Bài ôn cuối năm phần Hình học:

Giải bài 1 2 3 4 5 6 7 8 9 10 11 trang 90 91 92 sgk toán 7 tập 2

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 7 với giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 trang 88 89 90 sgk toán 7 tập 2!

“Bài tập nào khó đã có giaibaisgk.com“