Toán lớp 11

Ôn tập chương III: Trả lời câu hỏi 1 2 3 4 5 6 7 8 9 10 trang 120 sgk Hình học 11

Hướng dẫn giải Bài Ôn tập Chương III. Vectơ trong không gian. Quan hệ vuông góc trong không gian, sách giáo khoa Hình học 11. Nội dung bài trả lời câu hỏi 1 2 3 4 5 6 7 8 9 10 trang 120 sgk Hình học 11 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập hình học có trong SGK để giúp các em học sinh học tốt môn toán lớp 11.

Lý thuyết

1. §1. Vectơ trong không gian

2. §2. Hai đường thẳng vuông góc

3. §3. Đường thẳng vuông góc với mặt phẳng

4. §4. Hai mặt phẳng vuông góc

5. §5. Khoảng cách

6. Hệ thống hóa kiến thức quan hệ vuông góc trong không gian

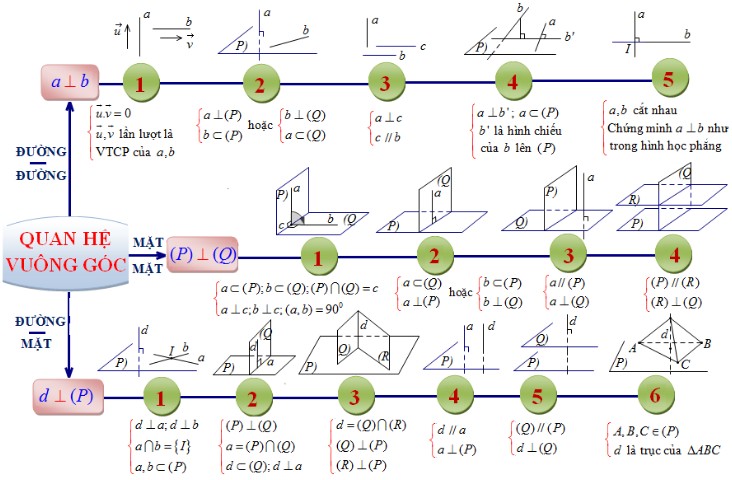
Dưới đây là phần Hướng dẫn trả lời câu hỏi 1 2 3 4 5 6 7 8 9 10 trang 120 sgk Hình học 11. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Câu hỏi Ôn tập chương III

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập hình học 11 kèm kèm câu trả lời chi tiết câu hỏi ôn tập 1 2 3 4 5 6 7 8 9 10 trang 120 sgk Hình học 11 của Bài Ôn tập Chương III. Vectơ trong không gian. Quan hệ vuông góc trong không gian trong mặt phẳng cho các bạn tham khảo. Nội dung chi tiết câu trả lời từng câu hỏi các bạn xem dưới đây:

Trả lời câu hỏi ôn tập 1 2 3 4 5 6 7 8 9 10 trang 120 sgk Hình học 11
Trả lời câu hỏi ôn tập 1 2 3 4 5 6 7 8 9 10 trang 120 sgk Hình học 11

1. Trả lời câu hỏi 1 trang 120 sgk Hình học 11

Nhắc lại định nghĩa vectơ trong không gian.

Cho hình lăng trụ tam giác \(ABC.A’B’C’\). Hãy kể tên những vecto bằng vectơ \(\overrightarrow {AA’} \) có điểm đầu và điểm cuối là đỉnh của hình lăng trụ.

Trả lời:

Định nghĩa vectơ trong không gian:

Vectơ trong không gian là một đoạn thẳng có hướng. Kí hiệu \(\overrightarrow{AB}\) chỉ véctơ có điểm đầu \(A\), điểm cuối \(B\). Véctơ còn được kí hiệu là \(\overrightarrow{a}\), \(\overrightarrow{b}\), \(\overrightarrow{c}\),… 

Hình lăng trụ tam giác \(ABC.A’B’C’\):

Các vectơ bằng vectơ \(\overrightarrow {AA’} \) có điểm đầu và điểm cuối là đỉnh của hình lăng trụ là: $\overrightarrow {BB’},\overrightarrow {CC’}$

(Vì: các cạnh bên của hình lăng trụ là các đoạn thẳng song song và bằng nhau)

2. Trả lời câu hỏi 2 trang 120 sgk Hình học 11

Trong không gian cho ba vectơ \(\overrightarrow a ,\overrightarrow b ;\overrightarrow c \) đều khác vectơ \(\overrightarrow 0 \) . Khi nào ba vectơ đó đồng phẳng?

Trả lời:

Định nghĩa: Trong không gian ba vectơ được gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.

Điều kiện để ba vectơ đồng phẳng: Cho \(\vec a, \vec b\) là hai vectơ không cùng phương và vectơ \(\vec c\). Ba vectơ \(\vec a, \vec b\) và \(\vec c\) đồng phẳng khi và chỉ khi có hai số thực m, n sao cho: \(\overrightarrow c = m.\overrightarrow a + n.\overrightarrow b .\)

3. Trả lời câu hỏi 3 trang 120 sgk Hình học 11

Trong không gian, hai đường thẳng không cắt nhau có thể vuông góc với nhau không? Giả sử hai đường thẳng \(a\) và \(b\) lần lượt có vecto chỉ phương là \(\overrightarrow u \) và \(\overrightarrow v \) . Khi nào ta có thể kết luận \(a\) và \(b\) vuông góc với nhau?

Trả lời:

Trong không gian, hai đường thẳng không cắt nhau có thể vuông góc với nhau không?

Trong không gian, hai đường thẳng vuông góc với nhau không nhất thiết phải cắt nhau. Vì vậy hai đường thẳng không cắt nhau vẫn có thể vuông góc với nhau.

Giả sử hai đường thẳng \(a\) và \(b\) lần lượt có vectơ chỉ phương là \(\overrightarrow u \) và \(\overrightarrow v \) . Khi nào ta có thể kết luận \(a\) và \(b\) vuông góc với nhau?

Đường thẳng \(a\) có vectơ chỉ phương \(\overrightarrow u \)

Đường thẳng \(b\) có vectơ chỉ phương là \(\overrightarrow v \)

\(a\) vuông góc với \(b\) khi và chỉ khi tích vô hướng của hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) bằng không hay \(a \bot b \Leftrightarrow \overrightarrow u .\overrightarrow v = 0\)

4. Trả lời câu hỏi 4 trang 120 sgk Hình học 11

Muốn chứng minh đường thẳng \(a\) vuông góc với mặt phẳng \((α)\) thì người ta cần chứng minh \(a\) vuông góc với mọi đường thẳng của mặt phẳng \(α\) hay không?

Trả lời:

Muốn chứng minh đường thẳng \(a\) vuông góc với mặt phẳng \((α)\) thì ta không cần phải chứng minh \(a\) vuông góc với mọi đường thẳng của mặt phẳng \((α)\).

Muốn chứng minh \(a ⊥( α)\) ta chỉ cần chứng minh $a$ vuông góc với hai đường thẳng cắt nhau nằm trong $(\alpha )$

Tức là: \(\left\{ \matrix{
a \bot b,b \subset (\alpha ) \hfill \cr
a \bot c,c \subset (\alpha ) \hfill \cr
b \cap c \hfill \cr} \right. \Rightarrow a \bot (\alpha )\)

5. Trả lời câu hỏi 5 trang 120 sgk Hình học 11

Hãy nhắc lại nội dung định lí ba đường vuông góc.

Trả lời:

Định lí ba đường vuông góc:

Cho đường thẳng d nằm trong mặt phẳng \(\left ( \alpha \right )\) và b là đường thẳng không thuộc \(\left ( \alpha \right )\) đồng thời không vuông góc với \(\left ( \alpha \right )\). Gọi b’ là hình chiếu vuông góc của b trên \(\left ( \alpha \right )\). Kho đó a vuông góc với b khi và chỉ khi a vuông góc với b’.

6. Trả lời câu hỏi 6 trang 120 sgk Hình học 11

Nhắc lại định nghĩa:

a) Góc giữa đường thẳng và mặt phẳng.

b) Góc giữa hai mặt phẳng.

Trả lời:

a) Góc giữa đường thẳng và mặt phẳng

Cho đường thẳng \(d\) cắt mặt phẳng \((α)\) tại điểm \(O\) và không vuông góc với \((α)\). Góc giữa đường thẳng \(d\) và mặt phẳng \((α)\) là góc tạo bởi đường thẳng và hình chiếu vuông góc \(d’\) của \(d\) trên mp \((α)\).

b) Góc giữa hai mặt phẳng

Giả sử hai mặt phẳng \((α)\) và \((β)\) cắt nhau theo giao tuyến \(c\). Từ điểm \(I\) bất kì trên \(c\), trong mặt phẳng \((α)\) ta dựng đường thẳng \(a\) vuông góc với \(c\) và trong mặt phẳng \((β)\) ta dựng đường thẳng \(b\) vuông góc với \(c\). Ta gọi góc giữa hai đường thẳng \(a\) và \(b\) là góc giữa hai mặt phẳng \((α)\) và \((β)\).

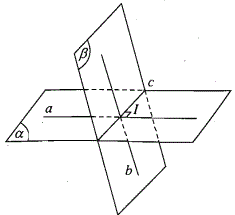
Chú ý: góc giữa hai mặt phẳng luôn luôn nhỏ hơn hoặc bằng \(90^0\).

7. Trả lời câu hỏi 7 trang 120 sgk Hình học 11

Muốn chứng minh mặt phẳng \((α)\) vuông góc với mặt phẳng \((β)\) người ta thường làm như thế nào?

Trả lời:

Các cách chứng minh mặt phẳng \((α)\) vuông góc với mặt phẳng \((β)\):

♦ Cách 1:

Chứng minh \((α)\) chứa một đường thẳng vuông góc với \((β)\) hoặc \((β)\) chứa một đường thẳng vuông góc với \((α)\)

\(\left\{ \matrix{
d \subset (\alpha ) \hfill \cr
d \bot (\beta ) \hfill \cr} \right. \Rightarrow (\alpha ) \bot (\beta )\)

♦ Cách 2:

Chứng minh góc giữa \((α)\) và \((β)\) bằng \(90^0\).

8. Trả lời câu hỏi 8 trang 120 sgk Hình học 11

Hãy nêu cách tính khoảng cách:

a) Từ một điểm đến một đường thẳng.

b) Từ đường thẳng \(a\) đến mặt phẳng \((α)\) song song với \(a\).

c) Giữa hai mặt phẳng song song.

Trả lời:

a) Khoảng cách từ một điểm đến một đường thẳng

Để tính khoảng cách từ điểm \(O\) đến đường thẳng \(a\) không đi qua \(O\), ta xác định mặt phẳng \((\alpha)\) và trong mặt phẳng này kẻ \(OH ⊥ a\). Độ dài \(OH\) chính là khoảng cách từ \(O\) đến đường thẳng \(a\).

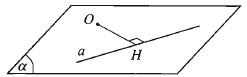$d(O;a) = OH$

b) Khoảng cách từ đường thẳng $a$ đến mặt phẳng $(\alpha)$

Để tính khoảng cách giữa đường thẳng \(a\) và mặt phẳng $(\alpha)$ song song với \(a\), ta lấy một điểm \(A\) bất kì thuộc đường thẳng \(a\). Khoảng cách \(AA’\) từ điểm \(A\) đến mặt phẳng $(\alpha)$ chính là khoảng cách giữa đường thẳng \(a\) với mặt phẳng $(\alpha)$ song song với \(a\).

$d(a;(α)) = d(O,(α)) = AA’ = BB’$

c) Khoảng cách giữa hai mặt phẳng song song

Để tìm khoảng cách giữa hai mặt phẳng $(\alpha)$ và \((β)\) song song với nhau, ta lấy một điểm \(M\) thuộc mặt phẳng $(\alpha)$ và tìm khoảng cách \(MM’\) từ điểm \(M\) đến mặt phẳng \((β)\)

$ d((α);(β)) = MM’$

9. Trả lời câu hỏi 9 trang 120 sgk Hình học 11

Cho \(a\) và \(b\) là hai đường thẳng chéo nhau. Có thể tính khoảng cách giữa hai đường thẳng chéo nhau bằng cách nào?

Trả lời:

♦ Cách 1:

Đưa về khoảng cách từ 1 điểm đển 1 mặt phẳng.

$d(a;b) = MN$

– Dựng mặt phẳng \((β)\) chứa đường thẳng \(b\) và song song với đường thẳng \(a\).

– Tìm khoảng cách từ một điểm \(M\) bất kì thuộc đường thẳng \(a\) đến mặt phẳng \((β)\).\

– Khi đó \(d\left( {a;b} \right) = d\left( {M;\left( β \right)} \right) = MN\)

♦ Cách 2: Dựng đường vuông góc chung.

Khi đó khoảng cách giữa $a$ và $b$ là độ dài đoạn vuông góc chung của hai đường thẳng đó.

$d(a;b) = MN$

10. Trả lời câu hỏi 10 trang 120 sgk Hình học 11

Chứng minh rằng tập hợp các điểm cách đều ba đỉnh của một tam giác \(ABC\) là đường vuông góc với mặt phẳng \((ABC)\) và đi qua tâm đường tròn ngoại tiếp tam giác \(ABC\).

Trả lời:

Lấy một điểm \(M\) bất kì trong không gian sao cho \(MA = MB = MC\). Từ \(M\) kẻ \(MO\) vuông góc với \((ABC)\). Các tam giác vuông \(MOA\), \(MOB\), \(MOC\) bằng nhau, suy ra \(OA = OB = OC\).

Do đó \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). Vậy các điểm \(M\) cách đều ba đỉnh của tam giác \(ABC\) nằm trên đường thẳng \(d\) đi qua tâm \(O\) của đường tròn ngoại tiếp tam giác \(ABC\) và vuông góc với mặt phẳng \((ABC)\).

Ngược lại, lấy một điểm \(M’ ∈ d\), với $d$ là đường thẳng qua tâm đường tròn ngoại tiếp tam giác $ABC$ và $\perp (ABC)$

Nối \(M’A, M’B, M’C\),

Do \(M’O\) chung và \(OA = OB = OC\) nên các tam giác vuông \(M’OA, M’OB, M’OC\) bằng nhau, suy ra \(M’A = M’B = M’C\),

Tức là điểm \(M’\) cách đều ba đỉnh \(A, B, C\) của tam giác \(ABC\).

Kết luận: Tập hợp các điểm cách đều ba đỉnh của tam giác \(ABC\) là đường thẳng vuông góc với mặt phẳng \((ABC)\) và đi qua tâm đường tròn ngoại tiếp tam giác \(ABC\).

Bài trước:

Bài tiếp theo:

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 11 với trả lời câu hỏi ôn tập 1 2 3 4 5 6 7 8 9 10 trang 120 sgk Hình học 11!

“Bài tập nào khó đã có giaibaisgk.com“