Ôn tập chương III: Giải bài 1 2 3 4 5 6 7 trang 121 122 sgk Hình học 11

Nội Dung

Hướng dẫn giải Bài Ôn tập Chương III. Vectơ trong không gian. Quan hệ vuông góc trong không gian, sách giáo khoa Hình học 11. Nội dung bài giải bài 1 2 3 4 5 6 7 trang 121 122 sgk Hình học 11 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập hình học có trong SGK để giúp các em học sinh học tốt môn toán lớp 11.

Lý thuyết

1. §1. Vectơ trong không gian

2. §2. Hai đường thẳng vuông góc

3. §3. Đường thẳng vuông góc với mặt phẳng

4. §4. Hai mặt phẳng vuông góc

5. §5. Khoảng cách

6. Hệ thống hóa kiến thức quan hệ vuông góc trong không gian

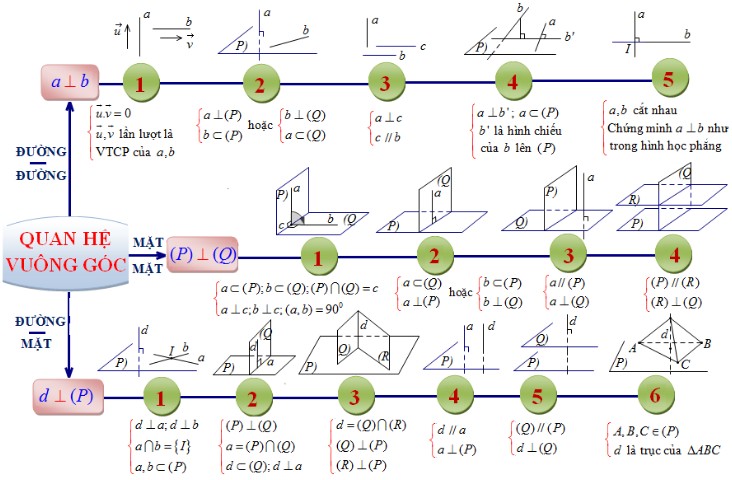
Dưới đây là phần Hướng dẫn giải bài 1 2 3 4 5 6 7 trang 121 122 sgk Hình học 11. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập Ôn tập chương III

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập hình học 11 kèm bài giải chi tiết bài 1 2 3 4 5 6 7 trang 121 122 sgk Hình học 11 của Bài Ôn tập Chương III. Vectơ trong không gian. Quan hệ vuông góc trong không gian trong mặt phẳng cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 6 7 trang 121 122 sgk Hình học 11

1. Giải bài 1 trang 121 sgk Hình học 11

Trong các mệnh đề sau, mệnh đề nào đúng?

a) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song

b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song

c) Mặt phẳng $(α)$ vuông góc với đường thẳng $b$ mà $b$ vuông góc với đường thẳng $a$, thì $a$ song song với $(α)$

d) Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song.

e) Hai đường thẳng cùng vuông góc với một đường thẳng thì chúng song song.

Bài giải:

a) Đúng

$\left\{ \matrix{
a \bot (P) \hfill \cr
b \bot (P) \hfill \cr} \right. \Rightarrow a//b$

b) Đúng

$\left\{ \matrix{
(P) \bot a \hfill \cr
(Q) \bot a \hfill \cr} \right. \Rightarrow (P)//(Q)$

c) Sai. Vì $a$ có thể thuộc mp $(α)$

d) Sai. Vì hai mp $(α)$ và $(β)$ cùng vuông góc với mp $(P)$ thì $(α)$ và $(β)$ vẫn có thể cắt nhau và trong trường hợp này thì giao tuyến của $(α)$ và $(β)$ vuông góc với mp $(P)$.

e) Sai. Vì hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì có thể không cùng thuộc một mặt phẳng, khi đó chúng cắt nhau.

2. Giải bài 2 trang 121 sgk Hình học 11

Trong các khẳng định sau đây, điều nào đúng?

a) Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại.

b) Qua một điểm có duy nhất một mặt phẳng vuông góc với mặt phẳng cho trước.

c) Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác cho trước.

d) Đường thẳng nào vuông góc với cả hai đường thẳng chéo nhau cho trước là đường vuông góc chung của hai đường thẳng đó.

Bài giải:

a) Đúng. Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c) Tính chất của khoảng cách giữa hai đường thẳng chéo nhau)

b) Sai. Qua một điểm, ta có thể vẽ được vô số mặt phẳng vuông góc với một mặt phẳng cho trước.

c) Sai. Vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước.

Để có khẳng định đúng, ta phải nói: “Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho“.

d) Sai. Vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường thẳng ấy.

3. Giải bài 3 trang 121 sgk Hình học 11

Hình chóp $S.ABCD$ có đáy là hình vuông $ABCD$ cạnh $a$, cạnh $SA$ bằng $a$ và vuông góc với mặt phẳng $(ABCD)$.

a) Chứng minh rằng các mặt bên của hình chóp là những tam giác vuông.

b) Mặt phẳng $(α)$ đi qua $A$ và vuông góc với cạnh $SC$ lần lượt cắt $SB, SC$ và $SD$ tại $B’, C’$ và $D’$. Chứng minh $B’D’$ song song với $BD$ và $AB’$ vuông góc với $SB$.

Bài giải:

a) Chứng minh rằng các mặt bên của hình chóp là những tam giác vuông.

Chứng minh $\Delta SAB$ vuông

Ta có: $SA\perp (ABCD),AB\subset (ABCD) ⇒ SA\perp AB ⇒ \Delta SAB vuông$

Chứng minh $\Delta SAD$ vuông

Ta có: $SA\perp (ABCD),AD\subset (ABCD) ⇒ SA\perp AD ⇒ \Delta SAD vuông$

Chứng minh $\Delta SBC$ vuông

$SA ⊥(ABCD)$ nên $AB$ là hình chiếu của $SB$ trên $mp(ABCD)$

$ABCD$ là hình vuông nên $BC ⊥AB$.

Ta có:

$\left. \matrix{
SA \bot (ABCD) \hfill \cr
BC \bot AB \hfill \cr} \right\}$

$⇒ SB⊥BC$ (theo định lí ba đường vuông góc)

$⇒ Δ SBC$ là tam giác vuông tại $ B$

Chứng minh $\Delta SCD$ vuông

$SA ⊥(ABCD)$ nên $AD$ là hình chiếu của $SD$ trên $mp(ABCD)$

$ABCD$ là hình vuông nên $CD ⊥AD$.

Ta có:

$\left. \matrix{
SA \bot (ABCD) \hfill \cr
CD \bot AD \hfill \cr} \right\}$

$⇒ SD⊥CD$ (theo định lí ba đường vuông góc)

$⇒ Δ SCD$ là tam giác vuông tại $ D$

b) Chứng minh $B’D’$ song song với $BD$ và $AB’$ vuông góc với $SB$.

Chứng minh $B’D’//BD$

Ta có: $\left.\begin{matrix} BD& \perp AC \\ BD& \perp SA \\ AC& \cap SA \end{matrix}\right\}\Rightarrow BD\perp (SAC)$

mà $SC\subset (SAC)\Rightarrow BD\perp SC$

Mặt khác: $(\alpha )\perp SC (gt)\Rightarrow BD//(\alpha )$

Ta có: $(SBD) \cap (\alpha ) = B’D’$

⇒ $B’D’//BD$

Chứng minh: $AB’\perp SB$

Vì $BC\perp (SAB),AB’\subset (SAB)\Rightarrow BC\perp AB’$ (1)

$SC\perp (\alpha ), AB’\subset (\alpha )\Rightarrow SC\perp AB’$ (2)

Từ (1) (2) suy ra $AB’ \perp (SBC)\Rightarrow AB’ \perp SB$

4. Giải bài 4 trang 121 sgk Hình học 11

Hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh $a$ và có góc $\widehat{ BAD} = 60^0$. Gọi $O$ là giao điểm của $AC$ và $BD$. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và $SO = {{3a} \over 4}$ . Gọi $E$ là trung điểm của đoạn $BC$ và $F$ là trung điểm của đoạn $BE$.

a) Chứng minh mặt phẳng $ (SOF)$ vuông góc với mặt phẳng $(SBC)$

b) Tính các khoảng cách từ $O$ và $A$ đến mặt phẳng $(SBC)$

Bài giải:

a) Theo giả thiết hình thoi $ABCD$ có: $\widehat{ BAD} = 60^0$ ⇒ $\widehat{ BCD} = 60^0$

Suy ra tam giác $BCD$ đều ⇒ $\widehat{ CBD} = 60^0$ hay $\widehat{ OBC} = 60^0$

$ABCD$ là hình thoi ⇒ $AC\perp BD \equiv O$ ⇒ $\Delta BOC$ vuông tại O có $E$ là trung điểm $BC$

⇒ $OE = EB = EC = \frac{1}{2}BC$ (tính chất đường trung tuyến ứng với cạnh huyền)

Xét tam giác $BOE$ có $BO=BE-cmt$ và $\widehat{ OBE} = 60^0$ nên tam giác $BOE$ đều

Có $F$ là trung điểm $BD$ ⇒ $OF$ đồng thời là đường cao ⇒ $OF ⊥BC$.

$\left. \matrix{
SO \bot (ABCD) \hfill \cr
{\rm{OF}} \bot {\rm{BC}} \hfill \cr} \right\} \Rightarrow SF \bot BC$

(Định lí 3 đường vuông góc)

$\left. \matrix{
SF \bot BC \hfill \cr
{\rm{OF}} \bot {\rm{BC}} \hfill \cr} \right\} \Rightarrow BC \bot (SOF)$

Mà $BC ⊂ (SBC)$

Suy ra $(SOF) ⊥ (SBC)$

b) Vì $(SOF) ⊥ (SBC)$ và hai mặt phẳng này giao nhau theo giao tuyến $SF$

nên từ $O$ ta kẻ $OH⊥SF$ ⇒ $OH⊥(SBC)$ ⇒ $d(O,(SBC))=OH$

Ta có:

$\eqalign{
& SO = {{3a} \over 4}{\rm{;OF = }}{{a\sqrt 3 } \over 4} \Rightarrow SF = {{a\sqrt 3 } \over 2} \cr
& OH.SF = SO.{\rm{OF}} \Rightarrow {\rm{OH = }}{{3a} \over 8} \cr} $

Gọi $K$ là hình chiếu vuông góc của $A$ trên $(SBC)$, ta có $AK//OH$

Trong $ΔAKC$ thì $OH$ là đường trung bình, do đó:

$AK = 2OH \Rightarrow AK = {{3a} \over 4}$

5. Giải bài 5 trang 121 sgk Hình học 11

Tứ diện $ABCD$ có hai mặt $ABC$ và $ADC$ nằm trong hai mặt phẳng vuông góc với nhau. Tam giác $ABC$ vuông tại $A$ có $AB = a, AC = b$. Tam giác $ADC$ vuông tại $D$ có $CD = a$.

a) Chứng minh các tam giác $BAD$ và $BDC$ đều là tam giác vuông

b) Gọi $I$ và $K$ lần lượt là trung điểm của $AD$ và $BC$. Chứng minh $IK$ là đường vuông góc chung của hai đường thẳng $AD$ và $BC$.

Bài giải:

a) Chứng minh các tam giác $BAD$ và $BDC$ đều là tam giác vuông

Chứng minh $\Delta BAD$ vuông

Theo giả thiết: $(ABC) ⊥ (ADC)$ mà hai mặt phẳng này giao nhau theo giao tuyến $AC$.

Ta lại có $BA ⊂ (ABC)$ và $BA⊥ AC$ nên $BA⊥(ADC)$

Vì $AB\subset (ADC) ⇒ BA⊥AD ⇒ ΔBAD$ vuông tại $A$

Chứng minh: $\Delta BCD$ vuông

$\left. \matrix{BA \bot (ADC) \hfill \cr AD \bot DC \hfill \cr} \right\} \Rightarrow BD \bot DC$

(Định lí 3 đường vuông góc)

$⇒ ΔBDC$ vuông tại $D$

b) Chứng minh $IK$ là đường vuông góc chung của hai đường thẳng $AD$ và $BC$.

Xét $\Delta ABC$ và $\Delta CAD$ có:

$\widehat{A}=\widehat{D}$

$AC$ chung

$AB=CD=a$

⇒ $\Delta ABC=\Delta CAD(c-g-c)$

⇒ $BI=CI$ (hai trung tuyến tương ứng của hai tam giác bằng nhau)

⇒ $\Delta IBC$ cân tại $I$

Có: $K$ là trung điểm $BC$ ⇒ $IK$ đồng thời là đường cao trong $\Delta IBC$

⇒ $IK \perp BC$ (1)

Chứng minh tương tự, ta có: $\Delta ABC=\Delta DCB(c-g-c)$

⇒ $AK=DK$

⇒ $\Delta KAD$ cân tại $K$

Có: $I$ là trung điểm $AD$ ⇒ $KI$ đồng thời là đường cao trong $\Delta KAD$

⇒ $KI \perp AD$ (2)

Từ (1) (2) ⇒ $IK$ là đường vuông góc chung của hai đường thẳng $AD$ và $BC$.

6. Giải bài 6 trang 122 sgk Hình học 11

Cho khối lập phương $ABCD.A’B’C’D’$ cạnh $a$.

a) Chứng minh $BC’$ vuông góc với mặt phẳng $(A’B’CD)$

b) Xác định và tính độ dài đoạn vuông góc chung của $AB’$ và $BC’$

Bài giải:

a) Chứng minh $BC’$ vuông góc với mặt phẳng $(A’B’CD)$

Ta có tứ giác $BCC’B’$ là hình vuông nên $BC’ ⊥ B’C$ (1)

Mặt khác $A’B’ ⊥ (BCC’B’)$ $⇒ A’B’ ⊥ BC’$ (2)

Từ (1) và (2) suy ra: $BC’⊥ (A’B’C’D’)$

b) Xác định và tính độ dài đoạn vuông góc chung của $AB’$ và $BC’$

Do $AD’//BC’$ nên mặt phẳng $(AB’D’)$ là mặt phẳng chứa $AB’$ và song song với $BC’$.

Ta tìm hình chiếu của $BC’$ trên $mp (AB’D’)$

Gọi $E, F$ là tâm của các mặt bên $ADD’A’$ và $BCC’B’$

Từ $F$ kẻ $FI ⊥ B’E$. Ta có $BC’ //AD’$ mà $BC’ ⊥ (A’B’CD)$

$⇒ AD’ ⊥ (A’B’CD)$ và $IF ⊂(A’B’CD)$

$AD’ ⊥ IF$ (3)

$EB’⊥IF$ (4)

Từ (3) và (4) suy ra : $IF ⊥ (AB’D’)$

Vậy $I$ là hình chiếu của $F$ trên $mp (AB’D’)$. Qua $I$ ta dựng đường thẳng song song với $BC’$ thì đường thẳng này chính là hình chiếu của $BC’$ trên mp $(AB’D’)$

Đường thẳng qua $I$ song song với $BC’$ cắt $AB’$ tại $K$. Qua $K$ kẻ đường thẳng song song với $IF$, đường này cắt $BC’$ tại $H$. $KH$ chính là đường vuông góc chung của $AB’$ và $BC’$.

Thật vậy: ${\rm{IF}} \bot (AB’D’)$

$\Rightarrow IF ⊥ AB’$ và $KH // IF$ suy ra $KH ⊥ AB’$

$\left. \matrix{
BC’ \bot (A’B’CD) \hfill \cr
{\rm{IF}} \subset {\rm{(A’B’CD)}} \hfill \cr} \right\} \Rightarrow \left. \matrix{
{\rm{IF}} \bot {\rm{BC’}} \hfill \cr
{\rm{KH//IF}} \hfill \cr} \right\} \Rightarrow KH \bot BC’$

Tam giác $EFB’$ vuông góc tại $F$, $FI$ là đường cao thuộc cạnh huyền nên

${1 \over {I{F^2}}} = {1 \over {FB{‘^2}}} + {1 \over {F{E^2}}}$ với

$\left\{ \matrix{
FB’ = {{a\sqrt 2 } \over 2} \hfill \cr
{\rm{EF = a}} \hfill \cr} \right.$

Ta tính ra: ${\rm{IF}} = {{a\sqrt 3 } \over 3} \Rightarrow KH = {\rm{IF = }}{{a\sqrt 3 } \over 3}$

7. Giải bài 7 trang 122 sgk Hình học 11

Cho hình chóp $S.ABCD$ có đáy hình hoi $ABCD$ cạnh $a$ có góc $\widehat{BAD}=60^0$ và $SA=SB=SD=\frac{a\sqrt{3}}{2}$

Cho hình chóp $S.ABCD$ có đáy là hình thoi $ABCD$ cạnh $a$, góc $\widehat {BAD} = 60^0$ và $SA = SB = SD = {{a\sqrt 3 } \over 2}$

a) Tính khoảng cách từ $S$ đến mặt phẳng $(ABCD)$ và độ dài cạnh $SC$

b) Chứng minh mặt phẳng $(SAC)$ vuông góc với mặt phẳng $(ABCD)$

c) Chứng minh $SB$ vuông góc với $BC$

d) Gọi $\varphi$ là góc giữa hai mặt phẳng $(SBD)$ và $(ABCD)$. Tính $\tan\varphi$

Bài giải:

a) Tính khoảng cách từ $S$ đến mặt phẳng $(ABCD)$ và độ dài cạnh $SC$.

Kẻ $SH⊥(ABCD)$

Do $SA = SB = SD$ suy ra $HA = HB = HC$

$⇒ H$ là tâm đường tròn ngoại tiếp tam giác $ ABD$.

Do $AB = AD = a$ và $\widehat{ BAD} = 60^0$ nên tam giác $ABD$ là tam giác đều cạnh $a$,

Ta có:

$\eqalign{
& AO = {{a\sqrt 3 } \over 2} \cr
& AH = {2 \over 3}AO \Rightarrow AH = {{a\sqrt 3 } \over 3} \cr} $

Trong tam giác vuông $SAH$, ta có: $SA = {{a\sqrt 3 } \over 2};AH = {{a\sqrt 3 } \over 3}$

Tính ra: $SH = {{a\sqrt {15} } \over 6}$

Ta cũng có: $HC = {{2a\sqrt 3 } \over 3}$

Trong tam giác vuông $SHC$:

$S{C^2} = S{H^2} + H{C^2}$

Suy ra: $SC = {{a\sqrt 7 } \over 2}$

b) Chứng minh mặt phẳng $(SAC)$ vuông góc với mặt phẳng $(ABCD)$

$\left. \matrix{
SH \bot (ABCD) \hfill \cr
SH \subset (SAC) \hfill \cr} \right\} \Rightarrow (SAC) \bot (ABCD)$

c) Chứng minh $SB$ vuông góc với $BC$

$\eqalign{
& S{C^2} = {{7{a^2}} \over 4}(1) \cr
& B{C^2} = {a^2}(2) \cr
& S{B^2} = {{3{a^2}} \over 4}(3) \cr} $

Từ (1), (2) và (3) ta có: $S{C^2} = B{C^2} + S{B^2}$

Theo định lí Pytago đảo, tam giác $SBC$ vuông tại $B$.

d) Gọi $\varphi$ là góc giữa hai mặt phẳng $(SBD)$ và $(ABCD)$. Tính $\tan\varphi$

Ta có:

$\eqalign{
& \left. \matrix{
DB \bot AC \hfill \cr
SH \bot (ABCD) \Rightarrow SH \bot DB \hfill \cr} \right\} \Rightarrow DB \bot (SAC) \cr
& \Rightarrow \left\{ \matrix{
DB \bot {\rm{OS}} \hfill \cr
{\rm{DB}} \bot AC \hfill \cr} \right. \cr} $

Suy ra: $\widehat{ SOH}$ là góc giữa hai mặt phẳng $(SBD)$ và $(ABCD)$

Do đó:

$\eqalign{
& \widehat{ SOH} = \varphi \cr
& \tan \varphi = {{SH} \over {OH}} \Rightarrow \tan \varphi = \sqrt 5 \cr} $

Bài trước:

Ôn tập chương III: Trả lời câu hỏi 1 2 3 4 5 6 7 8 9 10 trang 120 sgk Hình học 11

Bài tiếp theo:

Ôn tập chương III: Trả lời câu hỏi trắc nghiệm 1 2 3 4 5 6 7 8 9 10 11 trang 122 123 124 125 sgk Hình học 11

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 11 với giải bài 1 2 3 4 5 6 7 trang 121 122 sgk Hình học 11!

“Bài tập nào khó đã có giaibaisgk.com“