Nội Dung
Hướng dẫn giải Ôn tập cuối năm Đại số và Giải tích 11. Nội dung bài trả lời câu hỏi ôn tập cuối năm 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 trang 178 sgk Đại số và Giải tích 11 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập đại số và giải tích có trong SGK để giúp các em học sinh học tốt môn toán lớp 11.
Lý thuyết
1. Chương I. Hàm số lượng giác và phương trình lượng giác
2. Chương II. Tổ hợp – Xác suất
3. Chương III. Dãy số. Cấp số cộng và cấp số nhân
Dưới đây là Hướng dẫn trả lời câu hỏi ôn tập cuối năm 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 trang 178 sgk Đại số và Giải tích 11. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Câu hỏi Ôn tập cuối năm
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập đại số và giải tích 11 kèm câu trả lời chi tiết câu hỏi ôn tập cuối năm 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 trang 178 sgk Đại số và Giải tích 11 của Bài Ôn tập cuối năm Đại số và Giải tích 11 cho các bạn tham khảo. Nội dung chi tiết câu trả lời từng câu hỏi các bạn xem dưới đây:
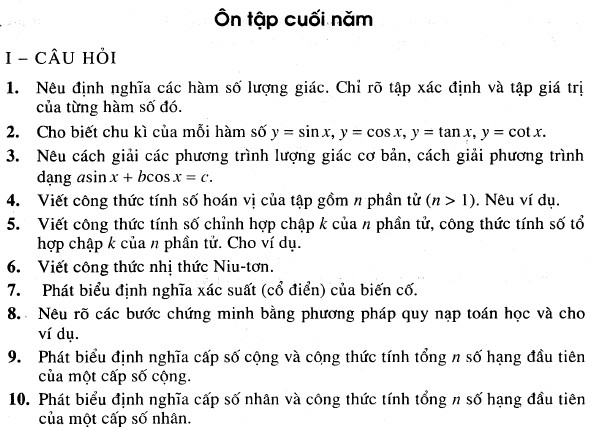
1. Trả lời câu hỏi 1 trang 178 sgk Đại số và Giải tích 11
Nêu định nghĩa các hàm số lượng giác. Chỉ rõ tập xác định và giá trị của từng hàm số đó.
Trả lời:
Hàm số sin: \(\sin: \mathbb R \rightarrow \mathbb R\)
\(x \mapsto y = {\mathop{\rm sinx}\nolimits} \)
Hàm số \(y = \sin x\) có tập xác định là \(\mathbb R\) và tập giá trị là \([-1, 1]\)
Hàm số cosin:
\(\eqalign{
{\mathop{\rm cosin}\nolimits} :&\mathbb R \to \mathbb R \cr
& x \mapsto y = \cos x \cr} \)
Hàm số \(y = \cos x\) có có tập xác định là \(\mathbb R\) và có tập giá trị là \([-1, 1]\)
Hàm số \(tan\):
\(\eqalign{
\tan :R\backslash {\rm{\{ }}{\pi \over 2} + k\pi ,k \in \mathbb Z&{\rm{\} }} \to \mathbb R \cr
& x \mapsto y = \tan x = {{\sin x} \over {\cos x}} \cr} \)
Hàm số \(y = \tan x\) có tập xác định là \(R\backslash \left\{ {{\pi \over 2} + k\pi ,k \in \mathbb Z} \right\}\) và có tập giá trị là \(\mathbb R\).
Hàm số cot:
\(\eqalign{
\cot: R\backslash \left\{ {k\pi ,k \in z} \right\} &\mapsto R \cr
& x \mapsto y = \cot x = {{\cos x} \over {\sin x}} \cr} \)
Hàm số \(y = \cot x\) có tập xác định là \(\mathbb R\backslash \left\{kπ, k ∈ \mathbb Z\right\}\) và có tập giá trị là \(\mathbb R\).
2. Trả lời câu hỏi 2 trang 178 sgk Đại số và Giải tích 11
Cho biết chu kì của mỗi hàm số \(y = sin x, y = cosx, y = tan x, y = cotx\)
Trả lời:
Chu kì của hàm số \(y = \sin x\) là \(T = 2 π\)
Chu kì của hàm số \(y = \cos x\) là \(T = 2 π\)
Chu kì của hàm số \(y = \tan x\) là \(T = π\)
Chu kì của hàm số \(y = \cot x\) là \(T = π\)
3. Trả lời câu hỏi 3 trang 178 sgk Đại số và Giải tích 11
Nêu cách giải các phương trình lượng giác cơ bản, cách giải phương trình dạng: \(a\sin x + b \cos x = c\)
Trả lời:
Phương trình lượng giác dạng cơ bản:
\(\eqalign{
& \sin x = \sin \alpha \Leftrightarrow \left[ \matrix{
x = \alpha + k2\pi \hfill \cr
x = \pi – \alpha + k2\pi \hfill \cr} \right.;k \in \mathbb Z \cr
& \cos x = \cos \alpha \Leftrightarrow x = \pm \alpha ,k \in \mathbb Z \cr
& \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi ,k \in \mathbb Z \cr
& \cot x = \tan \alpha \Leftrightarrow x = \alpha + k\pi ,k \in \mathbb Z \cr} \)
Hoặc:
\(\eqalign{
& \sin x = a \Leftrightarrow \left[ \matrix{
x = \arcsin a + k2\pi \hfill \cr
x = \pi – \arcsin a + k2\pi \hfill \cr} \right.;k \in \mathbb Z \cr
& \cos x = a \Leftrightarrow x = \pm \arccos a,k \in \mathbb Z \cr
& \tan x = a \Leftrightarrow x = \arctan a + k\pi ,k \in \mathbb Z \cr
& \cot x = a \Leftrightarrow x = {\rm{ar}}c\cot a + k\pi ,k \in \mathbb Z \cr} \)
Phương trình dạng : \(a \sin x + b \cos x = c\) (*)
Cách giải:
Chia cả hai vế của phương trình (*) cho \(\sqrt {{a^2} + {b^2}} \)
\(Pt \Leftrightarrow {a \over {\sqrt {{a^2} + {b^2}} }}\sin x + {b \over {\sqrt {{a^2} + {b^2}} }}\cos x = {c \over {\sqrt {{a^2} + {b^2}} }}(**)\)
Vì \({\left( {{a \over {\sqrt {{a^2} + {b^2}} }}} \right)^2} + {\left( {{b \over {\sqrt {{a^2} + {b^2}} }}} \right)^2} = 1\) nên ta đặt:
\(\cos \alpha = {a \over {\sqrt {{a^2} + {b^2}} }};\sin \alpha = {b \over {\sqrt {{a^2} + {b^2}} }}\)
Khi đó phương trình (**)
\(\eqalign{
& \Leftrightarrow \sin x.cos\alpha + \cos x.\sin \alpha = {c \over {\sqrt {{a^2} + {b^2}} }} \cr
& \Leftrightarrow \sin (x + \alpha ) = {c \over {\sqrt {{a^2} + {b^2}} }} \cr} \)
Đây là phương trình cơ bản ta đã biết cách giải.
4. Trả lời câu hỏi 4 trang 178 sgk Đại số và Giải tích 11
Viết công thức tính số hoán vị của tập gồm \(n\) phần tử (\(n > 1\)). Nêu ví dụ.
Trả lời:
Số hoán vị của n phần tử là \(P_n= n!\,\,\,\, (n > 1)\)
Ví dụ:
Từ các số \(1, 2, 3, 4\) ta có thể lập được \(4!\) số gồm \(4\) chữ số khác nhau.
5. Trả lời câu hỏi 5 trang 178 sgk Đại số và Giải tích 11
Viết công thức tính số chỉnh hợp chập \(k\) của \(n\) phần tử, công thức tính số tổ hợp chập \(k\) của \(n\) phần tử. Cho ví dụ.
Trả lời:
Số chỉnh hợp chập \(k\) của \(n\) phần tử là \(A_n^k = {{n!} \over {(n – k)!}}\)
Ví dụ: Cho \(10\) điểm \(A_1,A_2, …A_{10}\) phân biệt. Số vecto tạo bởi hai trong \(10\) điểm đã cho là \(A_{10}^2\).
Số tổ hợp chập \(k\) của \(n\) phần tử là: \(C_n^k = {{n!} \over {k!(n – k)!}}(n,k \in N,k \le n)\)
Ví dụ: Lớp 11A có 40 học sinh, có bao nhiêu cách chọn 6 học sinh để trực nhật (giả sử tất cả các học sinh đều bình đẳng về mọi mặt). Số cách chọn học sinh là: \(C_{40}^6\)
6. Trả lời câu hỏi 6 trang 178 sgk Đại số và Giải tích 11
Viết công thức nhị thức Niu-tơn.
Trả lời:
Công thức nhị thức Niu-tơn:
\({\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n – k}}{b^k}}\)
\(= C_n^0{a^n} + C_n^1{a^{n – 1}}b + C_n^2{a^{n – 2}}{b^2} + … + C_n^{n – 1}a{b^{n – 1}} \) \(+ C_n^n{b^n}\)
7. Trả lời câu hỏi 7 trang 178 sgk Đại số và Giải tích 11
Phát biểu định nghĩa xác suất (cổ điển) của biến cố.
Trả lời:
Giả sử \(A\) là một biến cố liên quan đến một phép thử chỉ có một số hữu hạn kết quả đồng khả năng xuất hiện, ta gọi tỉ số \({{n(A)} \over {n(\Omega )}}\) là xác suất của biến cố \(A\), kí hiệu là \(P(A)\).
Công thức tính: \(P(A) = {{n(A)} \over {n(\Omega )}}\)
8. Trả lời câu hỏi 8 trang 178 sgk Đại số và Giải tích 11
Nêu rõ các bước chứng minh bằng phương pháp quy nạp toán học và cho ví dụ.
Trả lời:
Các bước của phương pháp chứng minh quy nạp:
– B1: Chứng minh bài toán đúng với \(n = 1\)
– B2: Giả thuyết bài toán đúng với \(n = k\) (gọi là giả thiết quy nạp)
– B3. Chứng minh bài toán đúng v4ới \(n = k + 1\)
Khi đó kết luận bài toán đúng với mọi \(n\in {\mathbb N}^*\)
Ví dụ: Chứng minh rằng: với mọi \(n\in {\mathbb N}^*\) ta có:
\({1^2} + {2^2} + {3^2} + … + {n^2} = {{n(n + 1)(2n + 1)} \over 6}(1)\)
Bài giải:
Khi \(n = 1\) thì (1) trở thành \({1^2} = {{1(1 + 1)(2 + 1)} \over 6}\) đúng.
Giả sử (1) đúng khi \(n = k\), tức là:
\({1^2} + {2^2} + {3^2} + …. + {k^2} = {{k(k + 1)(2k + 1)} \over 6}\)
Ta chứng minh (1) đúng khi \(n = k + 1\), tức là phải chứng minh:
\({1^2} + {2^2} + {3^2} + …. + {(k + 1)^2} = {{(k + 1)(k + 2)(2k + 3)} \over 6}\)
Thật vậy :
\(\eqalign{
& {1^2} + {2^2} + {3^2} + …. + {k^2} + {(k + 1)^2} \cr
& = {{k(k + 1)(2k + 1)} \over 6} + {(k + 1)^2} \cr&= {{(k + 1)k(2k + 1) + 6(k + 1)} \over 6} \cr
& = {{(k + 1)(2{k^2} + 7k + 6)} \over 6} \cr&= {{(k + 1)(k + 2)(2k + 3)} \over 6} \cr} \)
Vậy (1) đúng khi \(n = k + 1\).
Kết luận: (1) đúng với \(n\in {\mathbb N}^*\)
9. Trả lời câu hỏi 9 trang 178 sgk Đại số và Giải tích 11
Phát biểu định nghĩa cấp số cộng và công thức tính tổng \(n\) số hạng đầu tiên của một cấp số cộng.
Trả lời:
Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn) mà trong đó, kể từ số hạng thứ hai, mỗi số hạng đều bằng tổng của số hạng đứng ngay trước nó và một số \(d\) không đổi, nghĩa là: \((u_n)\) là cấp số cộng \(⇔ ∀ n ≥ 2, u_n= u_{n+1}+ d\)
Số \(d\) gọi là công sai của cấp số cộng.
Tổng của \(n\) số hạng đầu tiên của một cấp số cộng là:
\({S_n} = {{n({u_1} + {u_n})} \over 2};{S_n} = {{\left[ {2{u_1} + (n – 1)d} \right]} \over 2}\)
10. Trả lời câu hỏi 10 trang 178 sgk Đại số và Giải tích 11
Phát biểu định nghĩa cấp số nhân và công thức tính tổng \(n\) số hạng đầu tiên của một cấp số nhân.
Trả lời:
Cấp số nhân là một dãy các số (hữu hạn hoặc vô hạn) mà trong đó, kể từ số hạng thứ hai, mỗi số hạng đều bằng tích của số hạng đứng ngay trước nó và một số \(q\) không đổi.
\((u_n)\) là cấp số nhân \(⇔ ∀ n ≥ 2, u_n= u_{n-1} .q\)
Số \(q\) gọi là công bội của cấp số nhân.
Tổng của \(n\) số hạng đầu tiên của một cấp số nhân là: \({S_n} = {{{u_1}(1 – {q^n})} \over {1 – q}}\,\,\,(q \ne 1)\)
11. Trả lời câu hỏi 11 trang 178 sgk Đại số và Giải tích 11
Dãy số \((u_n)\) thỏa mãn điều kiện gì thì được gọi là có giới hạn \(0\) khi \(n\) dần tới dương vô cực.
Trả lời:
Ta nói dãy số \((u_n)\) có giới hạn là \(0\) khi \(n\) dần tới dương vô cực, nếu \(|u_n|\) có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi.
Kí hiệu: \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = 0\) hay \(u_n\rightarrow 0\) khi \(n \rightarrow +∞\)
12. Trả lời câu hỏi 12 trang 178 sgk Đại số và Giải tích 11
Viết công thức tính tổng của một cấp số nhân lùi vô hạn.
Trả lời:
Công thức tính tổng của một cấp số nhân lùi vô hạn:
\(S = {{{u_1}} \over {1 – q}}(\,\,\,|q| < 1)\)
13. Trả lời câu hỏi 13 trang 178 sgk Đại số và Giải tích 11
Định nghĩa hàm số có giới hạn \(+ ∞\) khi \(x \rightarrow – ∞\)
Trả lời:
Cho hàm số \(y = f(x)\) xác định trên khoảng \((-∞, a)\)
Ta nói hàm số \(f(x)\) có giới hạn là \(+ ∞\) khi \(x \rightarrow – ∞\) nếu với dãy số \((x_n)\) bất kì, \(x_n< a\) và \(x_n \rightarrow – ∞\), ta có \(f(x_n) \rightarrow +∞\).
14. Trả lời câu hỏi 14 trang 178 sgk Đại số và Giải tích 11
Nêu các giới hạn đặc biệt của dãy số và của hàm số.
Trả lời:
Ta có:
\(\eqalign{
& \lim {1 \over n} = 0;\lim {1 \over {{n^k}}} = 0\,\,(k\in {\mathbb N}^*) \cr
& \lim{q^n} = 0\,\,(|q| < 1) \cr} \)
Nếu \(u_n= c\) ( \(c\) là hằng số) thì \(\lim u_n= \lim c = c\)
Các giới hạn đặc biệt của hàm số:
\(\mathop {\lim }\limits_{x \to + \infty } {x^k} = + \infty \) với \(k\in {\mathbb N}^*\).
\(\mathop {\lim }\limits_{x \to – \infty } {x^k} = – \infty \) nếu \(k\) là số lẻ.
\(\mathop {\lim }\limits_{x \to – \infty } {x^k} = + \infty \) nếu \(k\) là số chẵn.
15. Trả lời câu hỏi 15 trang 178 sgk Đại số và Giải tích 11
Nêu định nghĩa hàm số liên tục tại một điểm, trên một khoảng. Nêu hình ảnh hình học của một hàm số liên tục trên một khoảng.
Trả lời:
– Định nghĩa 1:
Hàm số \(f(x)\) xác định trên khoảng \(k\) được gọi là liên tục tại \(x_0∈ k\) nếu: \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\)
Hàm số không liên tục tại điểm \(x_0\) thì được gọi là gián đoạn tại điểm đó.
– Định nghĩa 2:
a) Hàm số \(f(x)\) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm trên khoảng đó.
b) Hàm số \(f(x)\) được gọi là liên tục trên \([a, b]\) nếu nó liên tục trên khoảng \((a, b)\) và \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = f(a);\mathop {\lim }\limits_{x \to {b^ – }} f(x) = f(b)\).
– Nhận xét:
Đồ thị của hàm liên tục trên một khoảng là một đường liền trên khoảng đó (hình dưới):

Hình dưới đây cho ví dụ về đồ thị của một hàm số không liên tục trên khoảng \((a, b)\)

16. Trả lời câu hỏi 16 trang 178 sgk Đại số và Giải tích 11
Phát biểu định nghĩa đạo hàm của hàm số \(y = f(x)\) tại \(x = x_0\)
Trả lời:
Cho hàm số \(y = f(x)\) xác định trên khoảng \((a, b)\) và \(x_0∈ (a, b)\)
Nếu tồn tại \[\mathop {\lim }\limits_{x \to {x_0}} {{f(x) – f({x_0})} \over {x – {x_0}}}\] thì giới hạn đó được gọi là đạo hàm của hàm số \(y = f(x)\) tại điểm \(x_0\) và kí hiệu \(f’(x_0)\)
Tức là \(f’\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) – f\left( {{x_0}} \right)}}{{x – {x_0}}}\)
17. Trả lời câu hỏi 17 trang 178 sgk Đại số và Giải tích 11
Viết tất cả các công thức tính đạo hàm đã học.
Trả lời:
Các công thức tính đạo hàm đã học:
\(\begin{array}{l}
+ )\,\,\left( {{x^n}} \right)’ = n{x^{n – 1}}\,\,\left( {n \in N,n > 1,x \in R} \right)\\
+ )\,\,\left( {\sqrt x } \right)’ = \frac{1}{{2\sqrt x }}\,\,\,\left( {x > 0} \right)
\end{array}\)
+) \((u + v – w) = u’ + v’ – w’\)
+) \((u.v.w)’ = u’.vw + u.v’w + u.v.w’\)
+) \( (u.v)’ = u.v’ + v.u’\)
+) \(({u \over v})’ = {{u.v’ – u’.v} \over {{v^2}}}(v = v(x) \ne 0)\)
+) \(({1 \over u})’ = – {{u’} \over {{u^2}}}(u = u(x) \ne 0)\)
18. Trả lời câu hỏi 18 trang 178 sgk Đại số và Giải tích 11
Giả sử hàm số \(y = f(x)\) có đạo hàm tại \(x_0\). Hãy viết phương trình tiếp tuyến của đồ thị hàm số tại điểm \(M_0(x_0, f(x_0))\).
Trả lời:
Phương trình tiếp tuyến của đồ thị hàm số \(y = f(x)\) tại điểm \(M_0(x_0, f(x_0))\) là: \(y – f(x_0)= f’(x_0)(x – x_0)\).
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 11 khác
- Để học tốt môn Vật lí lớp 11
- Để học tốt môn Sinh học lớp 11
- Để học tốt môn Ngữ văn lớp 11
- Để học tốt môn Lịch sử lớp 11
- Để học tốt môn Địa lí lớp 11
- Để học tốt môn Tiếng Anh lớp 11
- Để học tốt môn Tiếng Anh lớp 11 thí điểm
- Để học tốt môn Tin học lớp 11
- Để học tốt môn GDCD lớp 11
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 11 với trả lời câu hỏi ôn tập cuối năm 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 trang 178 sgk Đại số và Giải tích 11!
“Bài tập nào khó đã có giaibaisgk.com“
